The attached image shows the layout of streets in the centre of a small town, Midville, in which every line segment (e.g from A to B) is exactly 1 kilometer.
The City Council has just resurfaced all of the streets and now the line down the middle of each street must be repainted. The truck used for this purpose is very inefficient as far as petrol consumption is concerned, and so the Council would like to have the truck travel the shortest distance possible.
The truck is currently at the point A but after the job it must be parked at point B. What is the minimum distance that the truck can travel to complete this task? What route should be followed to achieve this minimum?
I would really love an explanation to this problem!
Question
Guest
The attached image shows the layout of streets in the centre of a small town, Midville, in which every line segment (e.g from A to B) is exactly 1 kilometer.
The City Council has just resurfaced all of the streets and now the line down the middle of each street must be repainted. The truck used for this purpose is very inefficient as far as petrol consumption is concerned, and so the Council would like to have the truck travel the shortest distance possible.
The truck is currently at the point A but after the job it must be parked at point B. What is the minimum distance that the truck can travel to complete this task? What route should be followed to achieve this minimum?
I would really love an explanation to this problem!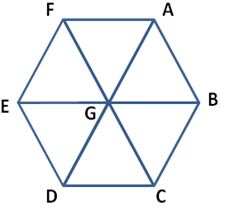
Link to comment
Share on other sites
14 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.