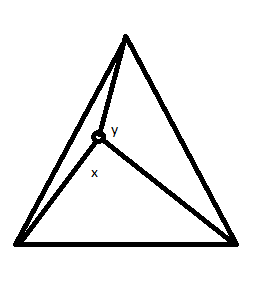BMAD

Suppose the post office only sold 5 cent and 7 cent stamps. Now, if the amount of postage on your mail had to be a precise amount equivalent to double of the distance (e.g. sending a letter five miles costs ten cents), what whole number locations are you not able to mail to?

Say 5939 is a "right" prime because it remains prime after dropping any number of digits from the right: 5939, 593, 59, and 5 are all prime. How many right primes are there less than 1000?

Four dogs are positioned at the corners of a square (d=1m), chase each other in clockwise direction with the same constant speed . As their target is moving, they will follow a curved path, eventually colliding in the center of the square. Why is the total length of the path just 1m?

Suppose g(x) = 3 + 1/x and f(g(x)) = 1/(x^2) what does f(x) equal?

yes, exactly.

The only day where you cannot have a partial car built is the 7th day. The other days must have a whole car built to meet your quota but you can have part of a car as long as you don't make two in a given day. You must build something each shift.

You are in charge of building cars, you are tasked to build exactly one car a day (no more, no less) and to be clear a partial car is as good as not building a car. Your shift is separated into two parts in which you could either build a whole, half, third, fourth, or fifth of a car in a given shift. By the end of the week you are to have built 7 cars with no partial cars left over. How many ways can this be done assuming a 7-day work week?

If the antiderivative of u^-1 = ln |u| + c then why does this not follow: integrate 1/(2x) dx set u =2x, then du = 2 dx, then dx = (1/2)du Then we could integrate (1/2)(1/u)du By the definition above we get 1/2 ln|u| + c which means that the integration of 1/(2x) = 1/2 ln|2x|| + c However, this is a false statement.

there is a faster time

5 college students need to cross a river in a small boat. Two of these students are on the rowing team and can cross it in one minute if either one or both are rowing. The other three are not and will take four minutes to cross even if they are with the rowing team members. The boat can only hold up to three people at a time. What is the shortest amount of time it will take to cross the river?

A thin four-foot long chain is suspended by its ends and nailed to a wall. Both nails are level with one another and parallel to the floor. Because of gravity, the middle of the chain is hangs down towards the floor. If the vertical length of the chain is two feet, what is the distance between the nails?

An odd number of soldiers are stationed in a field such that all the pairwise distances are distinct. Each soldier is told to keep an eye on the nearest other soldier. Prove that at least one soldier is not being watched.

Each person is betting $10 that they can pick the lowest positive integer that is not picked by anyone else. Each time an individual chooses a number they bet $10. Once everyone is satisfied that they picked enough numbers (as they can pick more than one) they show their choices. The individual with the lowest number that was not picked by anyone else, wins $100. You are competing against nine other logical and equally wealthy people, what would be your strategy to win the prize?

how are we defining touching?

Suppose you have a point within a equilateral triangle. If you were to connect each vertex to this point you would make three new line segments. Assume that you knew two of the angles formed at the point. Build a triangle out of these line segments. What can the two known angles tell us about the angles of this newly created triangle.

Twice

Stefan was on his way out the door to visit an old friend across the village when he realized that his grandfather clock had stopped and no longer displayed the correct time. This was the only clock in his home and the man owned no watches or other time-telling devices. Without disappointment Stefan left his home and walked roughly three miles to his friend's house. He glanced at the friend's wall clock as he entered the house and after visiting for a few hours set off back home along the same route. He walked at the same pace home and had no idea of knowing how long his trip back took him. Regardless, when Stefan got back home he immediately went to his grandfather clock and set it to the correct time. How did he know what time it was?

There was a flock of ducks flying in the sky. One ahead of the other two; one behind of the other two; one between the other two, and three in a row. How many ducks were flying?

I know what you mean but I don't think it is worded it right

Bill sold his motor scooter to Tom for $100. After driving it around for a few days Tom discovered it was in such a broken-down condition that he sold it back to Bill for $80. The next day Bill sold it to Herman for $90. What is Bill's total profit?

You and two of your friends would like to know the average of all of your salaries. You are each self-conscious about the amount of money you make and will not tell one another your salaries. What can you do to figure out the average salary?

You are in an empty room with a glass of water. The glass is a right cylinder that looks like it is about half-full, but you are unsure. What is the most accurate way, without spilling any water, to determine whether the glass is half-full, more than half-full, or less than half-full?

A man lives in Manhattan near a subway express station. He has two girlfriends, one in Brooklyn, one in the Bronx. To visit either girl he must take a train. To go to the one in Brooklyn, he takes a train on the downtown side of the platform, and to visit the one in the Bronx, he takes a train on the uptown side of the same platform. Since he likes both girls equally well, he simply takes the first train that comes along. In this way he lets chance determine whether he rides to the Bronx or to Brooklyn. The young man reaches the subway platform at a random moment each Saturday afternoon. Brooklyn and Bronx trains arrive at the station equally often--every ten minutes. Yet for some obscure reason, he finds himself spending most of his time with the girl in Brooklyn. In fact, on average, he goes there nine times out of ten. Why are the odds so heavily in favor of Brooklyn?

There is a solution. the problem can be solved by them either being parallel or not intersecting. Since this is proving challenging, lets just focus on the parallel situation for now. Maybe I will repost the question for not intersecting later.