-
Posts
1756 -
Joined
-
Last visited
-
Days Won
25
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by plasmid
-
-
On 3/10/2018 at 6:53 AM, plasmid said:
Does not compute when I try a Poisson distribution. I might be doing something wrong.
If we’re dealing with a Poisson distribution where the probability of having an interval x between two bags is proportional to e-x, then we need to re-calculate the probability of being a non-nearest neighbor segment. If you’re given a segment of length L, then the probability that it’s larger than an adjacent segment (or equivalently that an adjacent segment is smaller than L) is
Integral[x=0 to L] e-x / Integral[x=0 to infinity] e-x
[x=0 to L] -e-x / [x=0 to infinity] -e-x
(-e-L + e0) / (-e-infinity + e0)
(-e-L + 1) / (0 + 1)
1 - e-L
So the probability that both adjacent segments are smaller than L and therefore you have a non-nearest neighbor segment is the square of that, or
1 - 2e-L + e-2LIn my previous calculation, a segment would appear with uniform probability regardless of its length, but in this case the probability that you would observe a segment of length x is dependent on the value of x. To account for that, the ultimate value you want is the integral of [length of the segment] · [probability of seeing a segment of that length] · [probability that it’s a non-nearest neighbor segment] divided by the integral of [length of the segment] · [probability of seeing a segment of that length], which would be
Integral[x=0 to infinity] x·e-x·(1-2e-x+e-2x) / Integral[x=0 to infinity] x·e-x
Integral[x=0 to infinity] xe-x-2xe-2x+xe-3x / Integral[x=0 to infinity] xe-x
Split the terms in the numerator and use integration by parts to get
(-xe-x Integral -e-x + xe-2x Integral e-2x – (x/3)e-3x Integral (-1/3)e-3x) / (-xe-x Integral -e-x)
(-xe-x e-x + xe-2x (-1/2)e-2x – (x/3)e-3x (1/9)e-3x) / (-xe-x e-x)
(-xe-2x - (x/2)e-4x – (x/27)e-6x) / (-xe-2x)
Taking that integral from 0 to infinity then makes all of the e-nx terms be one at x=0 and zero at x=infinity. But then at x=infinity, you end up with terms that are infinity times zero :/SMH, continuing from that last line of formula...Spoiler(-xe-2x - (x/2)e-4x – (x/27)e-6x) / (-xe-2x)
1 + (1/2)e-2x + (1/27)e-4x
And getting the value of that integral over the range 0 to infinity is easy. [Infinity value] – [zero value] is
[1 + 0 + 0] – [1 + (1/2) + (1/27)] = -29/54I must have gotten positive/negative signs flipped somewhere, but I can’t find where.Edit: Nevermind, I think you have to calculate the value over the range of integration for the numerator and denominator separately, I don't think you can just divide through like that. And after looking it up, those limits go to zero so I've got an indeterminate 0/0 still.
-
Does not compute when I try a Poisson distribution. I might be doing something wrong.
SpoilerIf we’re dealing with a Poisson distribution where the probability of having an interval x between two bags is proportional to e-x, then we need to re-calculate the probability of being a non-nearest neighbor segment. If you’re given a segment of length L, then the probability that it’s larger than an adjacent segment (or equivalently that an adjacent segment is smaller than L) is
Integral[x=0 to L] e-x / Integral[x=0 to infinity] e-x
[x=0 to L] -e-x / [x=0 to infinity] -e-x
(-e-L + e0) / (-e-infinity + e0)
(-e-L + 1) / (0 + 1)
1 - e-L
So the probability that both adjacent segments are smaller than L and therefore you have a non-nearest neighbor segment is the square of that, or
1 - 2e-L + e-2LIn my previous calculation, a segment would appear with uniform probability regardless of its length, but in this case the probability that you would observe a segment of length x is dependent on the value of x. To account for that, the ultimate value you want is the integral of [length of the segment] · [probability of seeing a segment of that length] · [probability that it’s a non-nearest neighbor segment] divided by the integral of [length of the segment] · [probability of seeing a segment of that length], which would be
Integral[x=0 to infinity] x·e-x·(1-2e-x+e-2x) / Integral[x=0 to infinity] x·e-x
Integral[x=0 to infinity] xe-x-2xe-2x+xe-3x / Integral[x=0 to infinity] xe-x
Split the terms in the numerator and use integration by parts to get
(-xe-x Integral -e-x + xe-2x Integral e-2x – (x/3)e-3x Integral (-1/3)e-3x) / (-xe-x Integral -e-x)
(-xe-x e-x + xe-2x (-1/2)e-2x – (x/3)e-3x (1/9)e-3x) / (-xe-x e-x)
(-xe-2x - (x/2)e-4x – (x/27)e-6x) / (-xe-2x)
Taking that integral from 0 to infinity then makes all of the e-nx terms be one at x=0 and zero at x=infinity. But then at x=infinity, you end up with terms that are infinity times zero :/ -
This one

-
Spoiler
Suppose you have one guy that’s responsible for putting the bags on the conveyor belt, and the amount of time it takes him to put each subsequent bag on the belt is randomly drawn from a uniform distribution from 0 to 1 second. Also say the conveyor belt is moving at 1 meter per second to make the math easier. So you can work with a string of distances: x1, x2, x3, … and we’re looking for the ratio of (the sum of all terms xn where xn > xn-1 and xn > xn+1) divided by (the sum of all terms xn regardless of whether it's a non-nearest neighbor segment).
For any given value of xn, the probability that xn > xn-1 is simply the value of xn (since we’re dealing with a uniform distribution of values over a range from 0 to 1), and similarly the probability that xn > xn+1 is xn (since these numbers are randomly generated independently of each other). So the probability that xn is a non-nearest neighbor segment is the product of those two, or xn2.
Since the length of each segment is generated from a uniform distribution from 0 to 1, we can do an easy integral. To calculate the fraction of the conveyor belt that’s covered by non-nearest neighbor segments, I think we would want to take the integral of [length of the segment] · [probability that it’s a non-nearest neighbor segment] (which is x · x2 = x3) and divide that by the integral of [length of the segment].
Int[x=0 to 1] (x3 dx) / Int[x=0 to 1] (x dx)
[x=0 to 1] (x4/4) / [x=0 to 1] (x2/2)
(1/4) / (1/2) = 1/2That answer would very likely change if you used a different method to generate random distances between suitcases on the conveyor belt.
-
3 hours ago, bonanova said:
I can ask you to flip a coin for a 2nd time?
Flipping the same coin twice would be indistinguishable from not flipping it at all to your buddy. So you would just be exposing yourself to more nyaning without accomplishing anything.
-
It looks like harey and aiemdao have sort of similar strategies, and that the number of coins flipped would be up to log base 2 of the total number of coins. With harey's answer it could be less for certain numbers of coins in play, but not for all.
But if there are more than even a mere 32 coins, then you could be in for up to a solid hour of nyan-ing which might not be worth a bazillion bucks. Try for an approach with less, especially when the number of coins gets large.
-
I have a rare coin that’s worth a bazillion dollars and I’ll give you and a buddy a chance to win it.
I’ll bring you (but not your buddy yet) into a room where I have a bunch of coins lined up in a row, probably randomly distributed between being heads up and tails up, and I’ll tell you which coin among those is the bazillion dollar coin. Then you’ll exit the room and your buddy will come in through another entrance (so you can’t communicate after I tell you which is the bazillion dollar coin) and tell me which coin to give to the two of you.
That wouldn't be a very fair game, so you can also tell me to flip whichever coins you want before you leave the room and your buddy comes in. (I’m flipping them myself to make sure you don’t send codes with subtle placement of the coins or such tomfoolery.) But you have to watch 10 minutes of Nyan Cat for every coin I flip so you want to minimize the number of flips lest you go insane. I’m not saying beforehand how many coins will be in the room, and you only get one minute to tell your buddy a strategy (just words that can be spoken in under a minute, no written cheat sheets) before it’s time to play the game.
Clock starts now.
(I would credit the source of where I heard the original form of this puzzle that I'm modifying, but I can't remember the source any more.)
-
This might count as an ah-hah if it's true.
 Spoiler
SpoilerThe first car out on the road will of course be the first car in its cluster.
The second car will be the first car of its cluster if and only if it’s going slower than the first car, which will happen with probability 1/2.
The third car will be the first car of its cluster if and only if it’s going slower than both the first car and the second car, which will happen with probability 1/3.
The nth car will be the first car of its cluster with probability 1/n.And the number of clusters is, of course, equal to the number of first cars in a cluster.
So the expected number of clusters (if I’m understanding the meaning of expected values correctly, which I might not be) is Sum n=1-1024 (1/n) which is a tad over 7.5. -
Not an answer, but a description of a potential approach and what would still be needed to make it work since this has gone for a while without being cracked.
SpoilerIf you randomly place two points A and B in the circle:
Draw the line segment connecting those two points, then draw a stripe covering and perpendicular to that line segment. If the third point C is outside of that stripe, then the angle at either A or B will be obtuse. Also, cut out the circle with diameter from A to B from the stripe, because if point C is within that circle then the angle at C is obtuse. If point C is within what’s left of the stripe, then the triangle is acute (or right).
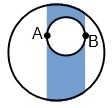
To figure the area of that stripe: Rotate the circle so the stripe is going vertically. Then measure the distance from the left edge of the stripe to the left edge of the circle, and from the right edge of the stripe to the right edge of the circle. The area that’s cut off from the stripe on either side can be calculated by taking the area of the circle’s wedge including that stuff that’s cut off, and subtracting the area of the isosceles triangle from the center’s origin that goes out to that area that’s cut off, as shown in the figure.
After calculating the area of those two edges that get cut off, you can calculate the area of the circle with diameter A to B, and then subtract all of those areas from the total area of the circle to get the area of the stripe.
That calculation would depend only on the x coordinates of points A and B after you rotate the circle to make line A-B parallel to the x-axis. If you can calculate the expected distribution of those two points’ x coordinates then the problem can be solved with those calculations. But describing that distribution given random placement of those two points has proven more difficult that I would’ve expected.
-
Probably not what you have in mind, but I realized part of my previous answer was superfluous so this is a little more elegant and gets rid of some hand waving.
SpoilerGiven a set with an equal number of red and blue points, it’s always possible to divide the set with a straight line into two subsets that each have an equal, positive number of red and blue points:
Pick a pivot point (not a red or blue point, just some unoccupied point) somewhere within the perimeter of the set of red and blue points and not colinear with any pair of the red or blue points, and draw a line through it that doesn’t intersect any of the red or blue points. If it divides the set into two subsets that each have an equal number of red and blue points, then you’re done. Otherwise, call the region with more red than blue points R and call the region with more blue than red points B. If you rotate the line 180 degrees around the pivot point then R and B will be swapped, so region R will have more blue than red and region B will have more red than blue. Since the pivot point is not colinear with any pair of red or blue points, the number of red or blue points in each region must increase or decrease by 1 if the line is rotated by a small enough angle, so during the rotation as region R goes from having more red to having more blue it must reach some angle where the number of red and blue points are equal. Since the pivot point is within the perimeter of the set of red and blue points, there must be at least one red and blue point in both subsets.
So you can start with the entire set of red and blue points and divide it into two subsets each with an equal number of red and blue points, then if either of those subsets have more than one point of each color you can divide that subset into two new subsets with equal numbers of red and blue to end up with three subsets, and keep repeating until you have many subsets each with one red and one blue point. Since the subsets will be convex, a line drawn between a red and a blue point within a subset won’t enter the regions of any other subsets, so you can connect the pair of points within each subset without worrying about overlap.
-
Spoiler
Draw a convex perimeter around the set of points (the shape of a taut rubber band with all the points inside). Unless every point on the perimeter is the same color, you will be able to find a segment on the perimeter with alternating colors at its vertices. Draw a line connecting those points, and you can remove them from the puzzle and be left with a smaller set of points where the line you just drew is outside of its convex perimeter and therefore won’t prevent you from drawing any more lines, so you can just repeat until you’ve joined all the points with lines.
But what if you reach a state where every point on the convex perimeter is the same color? Find a line that can divide the set of points into two separate sets of points that each have the same number of red and blue points, and then apply that algorithm to each of those two subsets. If the subsets also have monochromatic perimeters, divide those subsets into subsets and keep repeating the process as much as necessary until you can start connecting opposite color points.
Need a proof that a line must exist that can divide a set of points into two separate sets of points with equal numbers of red and blue? Draw any old line and it will divide the points into two regions; if they have equal numbers of red and blue points then you’re done, and if not then call the region with more blue than red points region B and call the region with more red than blue points R. If you gradually rotate the line 180 degrees, then regions B and R will be swapped so now B has more red than blue points and R has more blue than red. At some point during that rotation, if you’re allowed to nudge the line around a bit to make sure that only one point crosses the line at a time (I know I’m doing some hand waving but I think it’s still reasonable), the B and R regions must have reached a point where the number of blue and red vertices were equal.
-
On 2/9/2018 at 3:30 AM, Cygnet said:
Is it perhaps phalanges (finger bones)?
There are 14 bones considered to be phalanges, and it's odd that this number is even because the thumb only has two, otherwise we would have 15. Bones contain marrow, which creates blood cells - white and red/pink? Hands can be used to confer adulation (applause) when not used for slight (a dismissive gesture, or maybe flipping the bird). Woven tight (clasped together, fingers interwoven) mayhaps invoke (pray or beg for) serendipity.
But I can't explain the last couplet with this answer... at least nothing comes to mind.
Right on, Cygnet! Hopefully things make sense to readers with that answer in mind, but I'll go ahead and say what I was thinking for each of the clues.
SpoilerMy band of fourteen cultivates Fourteen phalanges, as you've found
Roses pink and white Fingernails
The oddly even adulates "Oddly even" = the thumb, which is odd because it's the only digit with an even number of phalanges, so oddly even
When not dispensing slight Which means these two lines are, as plainglazed said, referring to thumbs up or thumbs down
Woven tight, mayhaps invoke
Serendipity Prayer would work, but what I had in mind was crossed fingers to invoke good luck
Taken up by flame we stoke Something plainglazed alluded to in an earlier response -- a hand is taken up in marriage by a "flame"
In halo fittingly and is given a wedding ring -
None of the above, I’m afraid. A barrel (particularly if it’s a wine barrel) could fit most of the clues except for the oddly even adulating when not dispensing slight, and for wine I would have called the roses red and white instead of pink and white while for this riddle it definitely should be pink and white. I can say that thirteen is not involved in this riddle; the oddly even among the 14 is among a natural group of 14. And a bringer of good luck is involved, but I’m looking for something that can do everything from grow the pink and white roses, adulate or dispense slight, and fit the last two lines.
-
8 hours ago, Molly Mae said:
I like the double meaning that would give to the clue about adulating when not dispensing slight. But alas, I can't say that was planned. Looking for something with a clearer interpretation of being "oddly even" in light of the 14 clue, and another very related thing with a clear role in invoking good luck.
Maybe I shouldn't have used the word "band" in the first line; something like "gang" would work just as well without having connotations of a loop. -
Two more answers to add to ThunderCloud's.
Spoiler"Proof" that "all" triangles are obtuse
Place the first point of the triangle and call it point A, and place the second point and call it B. Create a coordinate system around A and B such that A falls on (0, 0) and B falls on (1, 0). Then place the third point of the triangle and call it C. The triangle will be obtuse if the x-coordinate of C is either less than zero or greater than one, and can only be acute or right if C is within the range [0-1] (and not even for all cases within that range). Since there’s a finite range of x-values where the triangle might not be obtuse and an infinite range where it would be obtuse, the odds of the triangle being obtuse are essentially 1."Proof" that ~64% of triangles are obtuse
Take the longest edge of the triangle and define a coordinate system such that the two vertices on that edge are at (0, 0) and (1, 0), and since that’s the longest edge, the triangle will be obtuse if and only if the opposing angle is obtuse. Since the longest edge has length 1, the other vertex must lie within a circle of radius 1 around (0, 0) and within a circle of radius 1 around (1, 0). Resorting to an online calculator, that area is about 1.228. Also, based on trigonometry (or maybe hand waving) I assert that if and only if the other vertex falls inside a circle at (0.5, 0) with radius 0.5 then the triangle is obtuse. That circle with radius 0.5 has area 0.7854. So the odds that the third vertex is within that area, and therefore that the triangle is obtuse, is 0.7854 / 1.228 ~= 64%.SpoilerYeah, I admit my first answer was sort of trolling :3
But even bogus answers can serve as lessons about what sort of faulty logic to be on guard for. -
I had to read up on that one a little bit. It certainly has the blossom like a rose and could go up in flames, but not what I'm going for with this one. Still looking for something something oddly even that adulates or slights, and a weaving invoking serendipity.
-
The four laws of card shifting
Spoiler1. If you see [2] [Empty] [1], then move card 1 onto card 2.
2. If you see any empty slot(s), move the card to the left of the empty slot into the empty slot, unless doing so would conflict with law 1.
3. If there are no empty slots and card 3 is in the far left slot, then move card 2 onto card 3.
4. If there are no empty slots and card 3 in NOT in the far left slot, then move card 3 one slot to the right.
-
Any stipulation for what would make one algorithm superior to another -- fewest / simplest number of commands, or fewest maximum number of moves to reach the goal?
I believe I can do it with four fairly simple commands that will take a maximum of 12 moves. -
Nah, no sports in particular or celebrities in general are involved in this riddle. This is something that everyone in the world will know about, although some of the clues refer to western cultural things that aren't quite completely universal.
-
After reading up on it a bit, at least some of the clues could be explained with that answer, but I've got to say that it would require far more specialized knowledge than I would put in a riddle meant for the general public.
-
Not silicon or glass, or anywhere along the elemental route. I had to do some research to see how well it would fit the clues, which obviously means it wasn’t what I had in mind. The fourteen makes sense with the atomic number, and I could see how silicon circuitry could invoke concepts of binary to explain the thing about adulating or dispensing slight. But there’s a particular reason why I chose pink and white as the colors of the “roses” that get cultivated, and I don’t think the part about serendipity when woven tight would apply to circuitry because determinism rather than luck is generally associated with electronics (at least in most people's minds to serve as a clue in a riddle).
-
Wow, that sure would give new meaning to the last couplet, with oxygen as the halo! Not what I have in mind, though; too many other clues would go without an explanation that I could see.
-
6 minutes ago, Molly Mae said:
Does that allow the other sheriff to make the arrest, though? That was the stumbling block I was having with my second approach.
Yep, in the next-to-last sentence you give him an instruction that lets him know which of his two suspects are guilty without letting the eavesdroppers know.
-
Getting cooler, neither a louse nor optics.


Coin hunt
in New Logic/Math Puzzles
Posted
Ok.
The technique that I know of has a small upper limit of how many coins you would ever need to flip, regardless of how many coins there are to choose from. You could always get the bazillion dollar coin with much less than an hour of nyan-ing.