Let P be a permutation on 12 objects

which has cycle length 12. As an

example, suppose P were given by

 1  2  3  4  5  6  7  8  9 10 11 12

 2  8  6 10  4  9 11  7 12  3  5  1

which tells us to move the object in the 1st position to the 2nd position, the object in the 2nd position to the 8th position, ..., and the object in the 12th position to the 1st position. We will use this to permute the 12 letters ABCDEFGHIJKL. Applying P to this yields LAJEKCHBFDGI. For this we write P(ABCDEFGHIJKL)=LAJEKCHBFDGI. We can continue to apply P so that P²(ABCDEFGHIJKL)=P(LAJEKCHBFDGI) and we can compute P(LAJEKCHBFDGI). Since P has cycle length 12, applying P over and over again 12 times will get us back to ABCDEFGHIJKL, written P¹²(ABCDEFGHIJKL)=ABCDEFGHIJKL. So, I can easily produce all 12 sequences of letters which powers of P can make when applied to ABCDEFGHIJKL. Now, suppose I do this with another permutation Q on 12 objects with cycle length 12. The 12 letter sequences which were produced (in alphabetical order -- NOT the order of their generation) is:

ABCDEFGHIJKL

BDGKAILFJECH

CGFLKAIEBDHJ

DKLCBJHIEAGF

EAKBJHCLFIDG

FIAJHCBKGLED

GLIHCBJADKFE

HFEILKADCGJB

IJBEFGDCLHAK

JEDAILKGHFBC

KCHGDEFJABLI

LHJFGDEBKCIA

Find all the possible permutations

which Q could be?

Nice problem

4 ways. There is a permutation Q that cycles through all 12 states given here, and the transformations Q⁵, Q⁷, and Q¹¹ also cycle through all 12 states.

I'm not sure how to improve the cycle length. I'd like to see the solution. Nice problem, by the way.

I don't quite see how that reference applies to this

problem. I intentionally didn't use the term 'cycle'

because that term is used in the way permutations can

be written. But your comment about disorder may be

a way of looking at it, if I understand you correctly.

I was going to post the following before I saw your

response -- it may help clarify things:

Bushindo's answer is way too small and phillip1882's is

way too big! Suppose, I had a permutation on 5 things.

Let P be the permutation that takes ABCDE to EABCD. Then

ABCDE -> EABCD -> DEABC -> CDEAB -> BCDEA -> ABCDE, and

so, P⁵=P. But what if P took ABCDE to CABED. Then,

ABCDE -> CABED -> BCADE -> ABCED -> CABDE -> BCAED -> ABCDE

shows that P⁶=P. So, 5 is too small because I found

a permutation on 5 things which requires six steps to return to

the start.

However, 5! = 120. I'd like to see someone find a permutation

on 5 things which requires 120 steps to get back to the start.

I can't.

You're right, it's way too small

I would say that the maximum is the product of the first 9 prime numbers

2*3*5*7*11*13*17*19*23 = 223092870

maximum cycle length of 100

I was talking about Bayes' treatment of prior probabilities especially when nothing is known about them. My point was that these are quite subjective.

I'd like to submit a point of view on this problem. I'd like to review the problem first. The crux of the debate, according to my skimming of the last 10 pages, boils down to this.

Let A(n), similar to superprismatic's definition, be the chance of initially having n white balls in the bag of 4.

We need to have the vector of probabilities [ P( A(2) ), P( A(3) ), P( A(4) ) ] to solve this problem. We are not given information about these states, and this is where mmiguel1 and superprismatic diverges.

mmiguel1 argues that in the lack of information about the balls-bag generation process, he will assume that the bag was generated by a binomial process with 4 trials and chance of black ball = .5.

superprismatic and the OP, and the CBSE board as well, argue that the uniform distribution is most representative of the lack of information, otherwise known as an un-informative prior in Bayesian statistics, and thus use the vector of probabilities [ P( A(2) ), P( A(3) ), P( A(4) ) ] = [ 1/3, 1/3, 1/3 ]. The uniform distribution is the oldest and simplest un-informative prior, so I can understand where this is coming from. The issue is that the uniform distribution is not the only un-informative prior there is (see http://en.wikipedia.org/wiki/Prior_probability#Uninformative_priors). There are a wide number of un-informative priors, and they probably would yield different answers. One example, for instance, would be to assume that each ball in the bag has a chance of being black p, where p belongs to the Beta distribution with the improper prior Beta(0,0).

superprismatic made the point that prior distribution, especially in case with no information, is subjective, which I think is where the discussion should have ended. However, my beef with the problem is that the CBSE puts this problem on a board exam, and presumably expects only 1 right answer, which is derived from assuming a uniform prior distribution as the non-informative prior. If the CBSE taught all their students to always assume the uniform as a non-informative prior, then this is a fair problem as a board exam. It is not, however, valid to post this problem to the brainden and board and expect .6 as the answer, just because the CBSE said so.

I tried this in Excel.

I started with $50. Each roll, I bet one dollar. For every 35 consecutive times I lost, I added another dollar to the bet. If I won then the number of losses started back at 0.

I decided to make exactly 250 bets. And record my cash at the end of the run.

I did this 25 times.

My average return for each "trip" to the casino was 259.12%

2 times, I went home no money.

2 other times, I went home with less than 50 dollars.

Subtracting my orginal $50 seed money, I netted $3189.

That is excellent result. 259% gain on your bankroll in roulette is great. Let's go to Vegas together this weekend.

please consider checking your excel code

As the number of iterations increases, the configuration

loses its memory of how it started and tends to randomness.

The number of ways six things can be taken three at a time is 20.

The configuration in question is unique. There is only one of them.

It's probability after 10 iterations [a sizeable number] is therefore

[approximately] 1/20.

Congrats to mmiguel1 and bonanova, who got the answer. I have a question about bonanova's method. While the answer is correct in this case, would the approach change at all if I change my state movement mechanism

From this: "an iteration as the act of randomly selecting a ball from bag A and transferring it to bag B, and then randomly selecting a ball from the four available balls in bag B, and transferring it back to bag A"

To this: "an iteration as the act of randomly selecting a ball from bag A and another ball from bag B, and then switching the two balls"

Intuition says that the final probability of 3 black balls in bag A will change with the change in state movement mechanism, but it is not apparent from the quick and dirty method.

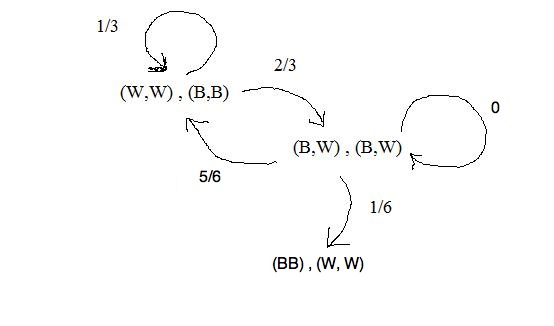
The path in Bushindo's state diagram from WW BB to BB WW multiplies out as 2/3 x 1/6 = 2/18 = 1/9.

The reciprocal is 9.

Or is that exactly what he said?

It seems to be a coincidence.

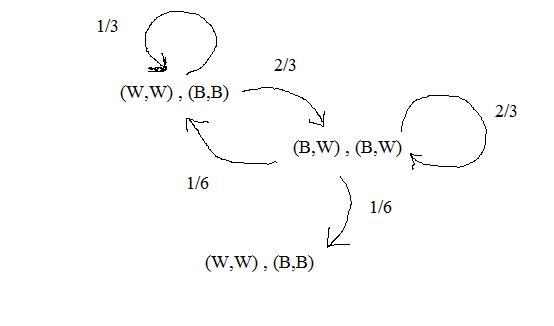
Suppose we modify the state movement mechanism so that BW BW no longer has a chance to go back to itself, and make P( WW BB | BW BW) = 5/6 instead of the original 1/6. We then have the following state diagram

The transition from WW BB to BW BW and from BW BW to BB WW are still the same: (2/3) and (1/6). However, since we are a lot more likely to go back to our starting point, the expected number of iterations to completion is now 15 instead of 9.

This is a variation on superprismatic's excellent puzzle White balls/ Black balls.

Suppose that we have two bags: bag A and bag B. Bag A contains 3 white balls, while bag B contains 3 black balls. We define an iteration as the act of randomly selecting a ball from bag A and transferring it to bag B, and then randomly selecting a ball from the four available balls in bag B, and transferring it back to bag A. Thus, at the end of each iteration, there are 3 balls in each bag.

Suppose we start with 3 white balls in bag A, and 3 black balls in bag B, and apply the iteration above 10 times. Now, if we open up bag A, what is the probability that we will see 3 black balls?

Yes, there are some fun problems on here. It's a nice site.

You have a very good, simple solution.

Not very important, but I think you missed an IL though

IL = (1/6)*(1) + (1/6)*( 1 + FI ) + (4/6)*( IL + 1 )

IL = (1/6)*(1) + (1/6)*( 1 + FI + IL) + (4/6)*( IL + 1 )

You obviously included it in your own calculation to get a value of 9.

When I try your method on the problem in the way I interpreted, I get the same value that I cranked out using probability rules and algebra.

Next time I come across a problem like this, I will choose your method.

Great job!

Nice catch. I didn't see that mistake. Your approach is one that i didn't think of. I solved this problem because I learned about Markov random chains before, so the framework is there. I find your solution to be more impressive since it is a brilliant and original application of probability rules and algebra. Well done.

Hello Bushindo, it has been a while. Superprismatic's Walter Penney puzzles were the best.

In this problem, you interpret that once you have placed a ball from A into B, when you select a ball in B to place in A, you may select any of the 3 in B.

Looking at the wording, that may be the correct interpretation.

I assumed each iteration meant swapping a ball between each bag.

"You randomly

pick a ball from bag A and place it

into bag B, then you randomly pick a

ball from bag B and place it into bag

A - this will be called an iteration."

because he uses the word "then", I think I originally had an incorrect interpretation.

May I ask how you calculated the expected value from your graph?

Hi mmiguel1, it really has been a while. Looks like you have been a very productive member on this board. I remember a couple of month ago you had your 1st post, and now you have almost the same post count as me.

Anyways, to compute the expected value from the graph, let's name the states. Let the first state [(W,W) , (B,B) ] be F, the intermediate state [(B,W) , (W,B) ] be I, and the last state [(B,B) , (W,W) ] be L. Let FL be the expected number of iterations from F to L, we can see that it can be decomposed into FL = FI + IL, where FI and IL are defined similarly to FL.

Examining the graph, we can write the following equation for FI

FI = 2/3 + (1/3)*( FI + 1 )

Solving for FI, we see that it takes an average of 3/2 iterations to go from first stage to intermediate stage. The equation for IL is

IL = (1/6)*(1) + (1/6)*( 1 + FI ) + (4/6)*( IL + 1 ).

We can now solve for IL, and compute FL = FI + IL.

Haven't been here for so long. I miss superprismatic's problems.

Let W stand for white balls, and B stands for black. We denote the content of a bag by ( color, color ), i.e. (W, W) for both whites. We represent the state of the problem at anytime as [ (color, color), (color, color) ], where the first parenthesis stands for bag A, and the second stands for

bag B. There are three states to this problem, which are [(W,W) , (B,B) ], [(B,W) , (W,B) ], and [(B,B) , (W,W) ].

We can easily compute the probability that any state will move to another during an iteration. For instance, from the beginning state [(W,W) , (B,B) ], for an iteration we can only move to the intermediate state [(B,W) , (W,B) ] with probability 2/3, and back to itself with probability 1/3. The directed graph for state movement is

From here, we can compute the expected number of iterations it takes to move from [(W,W) , (B,B) ] to [(B,B) , (W,W) ]. That number is 9.

Player 1 Wins


let the 3x3 matrix be


abc

def

ghi


Player 1 Starts, and no matter where he places his 1 the matrix can be rearranged as if he placed it in 'a'

this is based on the nature of a discriminant


for example if he places his 1 in 'f' so the matrix is


abc

de1

ghi


you can take a different matrix to play in and have the exact same results


abc..

de1de

ghigh

..cab


so you then have the matrix


1de

igh

cab


that the game takes place in, and because for now d,e,i,g,h,c,a,b are not yet defined we can just rewrite this matrix


1bc

def

ghi


so essentially player 1 always starts out by playing in 'a'


---


In order for player 0 to win he must make the matrix look like one of the following (with x representing a 0 or 1, because that place makes no difference to who wins.)


xxx	xxx	x0x	xx0

000	xxx	x0x	xx0

xxx	000	x0x	xx0



110	101	100	110	101

110	010	011	001	101

001	101	011	110	010

---


Player 1 Then tries to make every one of these matrices impossible by playing 1's where the 0's are in the above matrices


On turn 2 when player 0 places a 0 on the matrix, he can either leave himself 6 or 7 possible winning matrices. (Neither option will ultimately win... 

but lets assume he plays to get 7 possibilities) which would be playing in 'b', 'c', 'd', or 'g'


Player 1's next move can be made to remove 3 (or 4 in some cases) more possible matrices. Leaving Player 0 with a maximum of 4 matrices


Now when player 0 goes he must limit himself by at least two more, leaving only 2 possible matrices.


Player 1 then blocks one of them.


Player 0 places his 3rd 0, and is one place shy of victory when Player 1 places his fourth 1 to block the last possible winning matrix for player 0.


Thus player 1 will always win.


(I hope that makes sense, it does to me...)

Some comment

The argument is that player 1 and player 0 compete on acheiving and denying possible winning matrices. However, it seems the argument above assumes player 1 and player 0 can make their moves independently of one another. Player 0, however, can force player 1 to make certain moves. For instance, player 0 automatically wins if he get a horizonal or vertical row of all 0's. Therefore, whenever player 0 has a two 0's in a row or column, player 1 is forced to fill in the respective row or column with a 1 to block certain defeat. That may change the dynamic of the game tree.

Well, it seems nobody wants to provide a proof so

Although I can't see a good way to prove it using induction, I do have a fairly simple proof:

Denote the 17-long sequence by S_i for i from 1 to 17. Assume no such 5-long increasing or decreasing subsequence can be made.

Label each S_i with a pair of numbers (D_i,I_i) where D_i is the length of the longest decreasing subsequence

ending at S_i, and I_i is the length of the longest increasing subsequence ending at S_i. Now, 1 <= D_i <= 4

and 1 <= I_i <= 4 by our assumption that no 5-long can be made. So, there are only 4*4=16 possible pairs, (D_i,I_i).

But since there are 17 numbers S_i with associated labels (D_i,I_i), there must be at least one pair of duplicate labels.

So, suppose the duplicates are (D_j,I_j) and (D_k,I_k) with j<k. If S_j<S_k then the increasing

subsequence ending at S_j can have S_k appended to it, thereby making it one longer (and increasing I_k by 1). But I_k

is already as large as possible, by definition. A similar thing happens to D_k if S_j>S_k. So, duplicate labels cannot

occur, and we come to a contradiction. So our assumption that there is no 5-long increasing or decreasing subsequence must be wrong.

That's a nice proof. I didn't think of that. Here's a clumsier proof using induction

Without loss of generality, let's assume we already know that this statement is true for subsequence of length 4 from any 10 distinct integers.

Given a set of 17 distinct integers, we show that in the first 16 integers, there are 7 increasing or decreasing length-4 subsequences with different end-points. We do this by the following method

1) Select the first 10 integers, there is 1 increasing or decreasing sequence of length 4. Let the last integer of this sequence be called L₁.

2) Select the first 11 integers, and then removing L₁. We have another set of 10 integers. There is 1 increasing or decreasing subsequence with a different last integer, call this L₂.

3) Select the first 12 integers, and then removing L₁ and L₂. We have another set of 10 integers. There is 1 increasing or decreasing subsequence with a different last integer L₃.

4) Repeating step 3) up until the 16th integer, we have 7 different subsequences of length 4 with 7 different last integers.

Of these 7 subsequences, there must be 4 sequences that are of the same direction (increasing or decreasing). Without loss of generality, let's assume that we have 4 increasing sequences. Assuming no qualifying subsequence of length 5 in the first 16 integers, the last integers of these 4 increasing subsequence must form a decreasing subsequence of length 4. Consequently, when we add in the 17th integers, there is bound to be a subsequence of length 5.

I didn't feel inclined to prove the opening statement, which is that we can get subsequences of 4 out of 10 integers. But the outline above can be generalized enough to make the induction process fully rigourous.

I saw this in a test long ago.

In Determinant Tic-Tac-Toe, Player 1 enters a 1 in an empty 3×3 matrix. Player 0 counters with a 0 in a vacant position, and play continues in turn until the 3×3 matrix is completed with five 1’s and four 0’s. Player 0 wins if the determinant is 0 and player 1 wins otherwise. Assuming both players pursue optimal strategies, who will win and how?

Erdos and another settled this before I was born. I learned the theorem on my Polish mother's knee!

That's some childhood you got, maybe it's a polish thing. I got mostly spanks on my mother's knee. I'll supplement the hint that magician gave earlier

The same relationship applies to sequences of 4 from 10 distinct numbers (and also sequences of 3 from 5 integers ). From here, induction may be applied.

I saw this problem in a test long ago.

Assume that we have a sequence of 17 distinct integers. Show that there exist at least 1 subsequence of 5 integers that form an increasing or decreasing sequence.

For instance, let the sequence of 17 distinct integers be

9, 13,  6,  1, 11,  7, 16,  3, 15, 10,  2,  5, 12,  4, 14,  8, 17

Then there is a increasing subsequence of length 5 in (1,3,5,8,17). There is also a decreasing subsequence of (16,15,10,5,4). Show that the statement in the second paragraph is true for all sequences of 17 distinct integers.

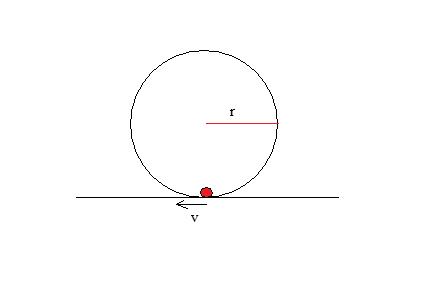
Let's say there's a circular track placed perpendicular to the ground as in the following image

The track has radius r. At the bottom of the track, there is a ball with horizontal velocity v. What is the minimum velocity v such that the ball will travel along the track to make a full circle without falling off the track at any point. Assume that there is no friction, and that the radius of the ball is very small relative to the radius of the track.

It is a 9. I counted.

http://gimbo.org.uk/texts/ten_thousand_factorial.txt

The 2500th digit from right to left is actually an even number.

As psychic mind have demonstrated before, there are 2499 trailing zeroes because there are 2499 factors of 5's. However, there are many more factors of 2's, which indicates that the 2500th digit must be even. A closer look at the file in babbagadoosh6's spoiler indicates that the 2500th digit is actually an 8. The cited digit of 9 in the last post is actually the 2503th digit.

Those who are intrigued by this problem may be interested in this theorem

Green–Tao theorem

I have written a detailed derivation of the answer to this problem. You can find it in .pdf format in the following link.

Answer

Nice solution. It's good to see another Latex user on this board.

I don't know how to save all but 1 like the original problem but I can save all but n-1 (where n is the number of hat colors)

say the colors are a,b,c,....,y,z then the 1st person says y or z if they see an even or odd number of 'a' color hats. The second person then says a if that is their hat color, otherwise says y or z if they see an even or odd number of 'b' color hats. If the 2nd say 'a' then the 3rd says either 'a' if they know that or even/odd for the 'b' color hats but if the 2nd declared the even/odd of 'b' hats then the 3rd now knows if that have 'a' or 'b' color hat (and says 'a' or 'b' if they have it or otherwise does the same for 'c' color hats. So as long as the prisoners have great memories and keep track (and can see all the hats in front of them and can count), all but n-1 prisoners are guarenteed saved and the probability of the non-guarenteed goes 1/n,1/(n-1),...,1/2

General N-hats solution

Let's consider the case of N different types of hats. Without lack of generality, let the types of hat be indicated by numbers from 0 to (N-1), rather than the color. The general algorithm goes as follows

1) Last prisoner sums up the value of all the hats he sees, divide the total by N and take the remainder, say that remainder out loud. His chance of survival is 1/N

2) Next prisoner looks at all the hats he sees and compute the remainder also. Computing his own hat color is simple. For instance, if there are 4 hats, and the sequence goes as follows (0,2,1,3), the last person (number 3) would say ((0+1+2) mod 4 ) = 3. The next person sees (( 0 + 2) mod 4) = 2, so he would know that his hat is number 1.

3) Repeat step 2 down to the first prisoner in line. Each person will need to keep track of the numbers previously announced. Chance of survival for all prisoners besides the first one is 100%.

It is possible to construct a guaranteed non-losing strategy, regardless of what the other guy does.

Let's say that I only use numbers from 1 to 5. At each turn, I draw a number from the following distribution, where P(n) is the chance of drawing number n

( P(1), P(2), P(3), P(4), P(5) ) = ( 1/16, 5/16, 4/16, 5/16, 1/16 )

A look will show that regardless of what the other guy does or what numbers he pick, I never have less than a 1/2 chance of winning. I suspect that there are slightly more optimal probability distribution. I'll update with more info later.

Sorry for not updating earlier as promised. I was away at camp for three days without access to internet.

As far as memoryless strategy goes, the strategy posted in the previous post guarantees a expected loss of 0 if the opponents plays numbers between 1-5. If the opponent plays numbers > 5, then the previous strategy has positive expecting winnings. This strategy works regardless of whatever the strategy the opponent does. I was thinking that slightly more optimal strategy might exist that has worst case expected loss of 0, and positive expected winnings against some numbers inside the set of 1,2,...5. However, no such strategy exist, since that would contradict with the strategy in the previous post. The strategy posted is the only one that has non-losing property. Any other strategy, i.e. any probability distribution in 5-dimensional vector, can be beaten by some other strategy vector in the same space.

That said, an optimal strategy for this game is probably to start playing with the guaranteed non-losing strategy above, and observe the opponent's moves. Once you have a good idea of his strategy (i.e. the probability distribution of his numbers, or whether he uses information from previous rounds ), you can take advantage of it, assuming that he doesn't use the same non-losing strategy.

What ever strategy A chooses, B can choose the same. So the expected winnings/losses for both are same.

It is possible to construct a guaranteed non-losing strategy, regardless of what the other guy does.

Let's say that I only use numbers from 1 to 5. At each turn, I draw a number from the following distribution, where P(n) is the chance of drawing number n

( P(1), P(2), P(3), P(4), P(5) ) = ( 1/16, 5/16, 4/16, 5/16, 1/16 )

A look will show that regardless of what the other guy does or what numbers he pick, I never have less than a 1/2 chance of winning. I suspect that there are slightly more optimal probability distribution. I'll update with more info later.

Absolutely correct, ljb, I did realize your answer was a mere typo. Well done. Of course proving it is a different matter. Believe it or not, the solution is just as easy when at each step the probability of A winning a coin is p:q not 50:50.

Here's a way to derive the answer using matrices. This probably isn't the solution you had in mind. I'd like to know that solution, though.

Let the total number of coins be T = p + q.

Let P(0) be the chance that A wins the game when he has 0 coin left. Of course, we know that P(0) = 0

Let P(1) be the chance that A wins the game when he has 1 coin left

...

Let P(n) be the chance that A wins the game when he has n coins

We can write the following system of equation

P(0)        =    P(0)               = 0

P(1)        = .5 P(0)     + .5 P(2) 

P(2)        = .5 P(1)     + .5 P(3) 

...

P(T - 1)    = .5 P(T - 2) + .5 P(T) 

P(T)        =                  P(T) = 1

We can write the above as a matrix equation A * x = x Where x = (P(0), P(1), ..., P(T) )' is a column vector of all the probabilities. A is a matrix of zeroes with 1's at A[1,1] and A[T,T], and .5's immediately to the left and right of the diagonal for rows 2 to (T-1). The solution to our problem is the eigenvector of A that correspond to the eigenvalue 1. Here's an example with T = 5

A = 

     [,1] [,2] [,3] [,4] [,5] [,6]

[1,]  1.0  0.0  0.0  0.0  0.0  0.0

[2,]  0.5  0.0  0.5  0.0  0.0  0.0

[3,]  0.0  0.5  0.0  0.5  0.0  0.0

[4,]  0.0  0.0  0.5  0.0  0.5  0.0

[5,]  0.0  0.0  0.0  0.5  0.0  0.5

[6,]  0.0  0.0  0.0  0.0  0.0  1.0


eigenvalues

[1]  1.000000  1.000000 -0.809017  0.809017 -0.309017  0.309017


eigenvectors

     [,1] [,2]      [,3]      [,4]      [,5]      [,6]

[1,]  1.0  0.0  0.000000  0.000000  0.000000  0.000000

[2,]  0.8  0.2 -0.371748 -0.371748 -0.601501 -0.601501

[3,]  0.6  0.4  0.601501 -0.601501  0.371748 -0.371748

[4,]  0.4  0.6 -0.601501 -0.601501  0.371748  0.371748

[5,]  0.2  0.8  0.371748 -0.371748 -0.601501  0.601501

[6,]  0.0  1.0  0.000000  0.000000  0.000000  0.000000

So, we see that for T = 5, (P(0), P(1), P(2), P(3), P(4), P(5) ) = (0, 1/5, 2/5, 3/5, 4/5, 5/5). It is relatively easy to discern the overall formula for P(n) from the this example. To be completely rigorous, one can directly compute the eigenvectors from a general A of size n x n, but I'd say that's a tag team job, if anyone wants to do it.

Of course, an easier way to prove the general formula would be to show that for matrix A of size N x N, where A has the special form specified above, the vector v = ( 0/N, 1/N, ...., N/N) is an eigenvector with eigenvalue 1. That is, the vector v satisfies the equation A*v = v. That should be a bit easier.