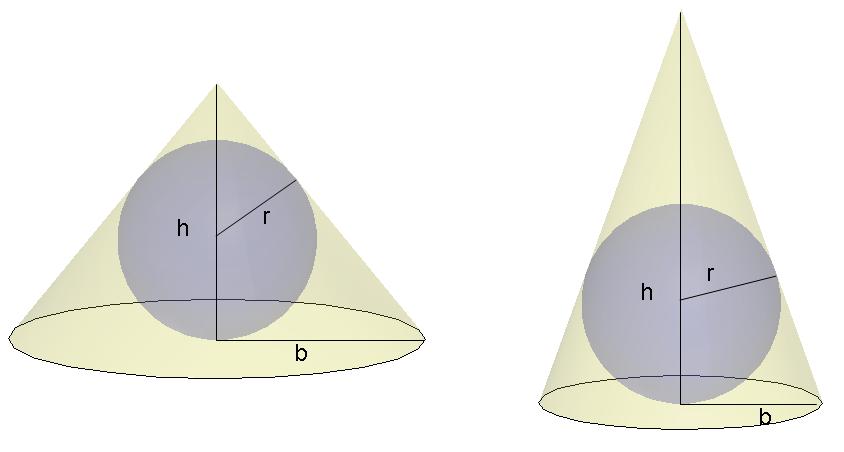
A sphere of radius r is inside a cone as shown in the figure. If the cone height h is made larger, then the radius of the base b needs to be shorter in order for the sphere to be in contact with the sides and the bottom of the cone.
Find h (as a function of r) That minimizes the volume of the cone. In other words find the the height of the cone with minimum volume that satisfies the conditions shown in the figure.
P.S. This if my first post. English is my second language and I am Engineer not a mathematician.
Question
Guest
A sphere of radius r is inside a cone as shown in the figure. If the cone height h is made larger, then the radius of the base b needs to be shorter in order for the sphere to be in contact with the sides and the bottom of the cone.
Find h (as a function of r) That minimizes the volume of the cone. In other words find the the height of the cone with minimum volume that satisfies the conditions shown in the figure.
P.S. This if my first post. English is my second language and I am Engineer not a mathematician.
Edited by momo567Link to comment
Share on other sites
9 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.