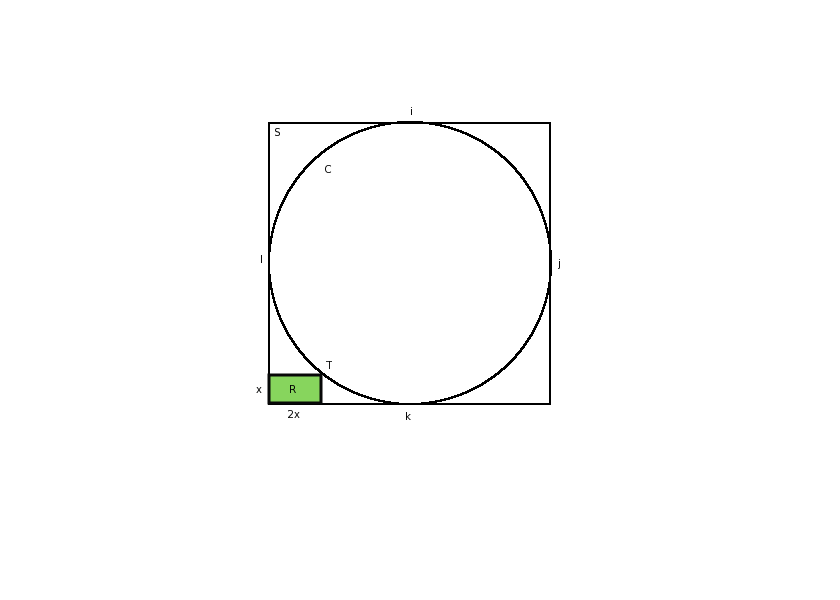
Guest Posted December 12, 2008 Report Share Posted December 12, 2008 (edited) The circle C is inscribed in the square S, i.e. they intersect at points i,j,k,l. The rectangle R has sides of length x and 2x, has one corner in common with S, and touches C at point T. How many such rectangles can fit inside the square? [Edit] How many *non-overlapping* rectangles the size of R can fit in an *empty* square the size of S. [/Edit] Edited December 12, 2008 by xucam Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 The circle C is inscribed in the square S, i.e. they intersect at points i,j,k,l. The rectangle R has sides of length x and 2x, has one corner in common with S, and touches C at point T. How many such rectangles can fit inside the square? Eh...4? Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 Eh...4? No, the circle doesn't get in the way, it is there to give you scale. Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 The circle C is inscribed in the square S, i.e. they intersect at points i,j,k,l. The rectangle R has sides of length x and 2x, has one corner in common with S, and touches C at point T. How many such rectangles can fit inside the square? Need more info: Can rectangle overlap? Do they have to be outside the circle? Can they be in the circle as long as they don't cross it? There are several possible answers with the information given in OP. Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 (edited) Need more info: Can rectangle overlap? Do they have to be outside the circle? Can they be in the circle as long as they don't cross it? There are several possible answers with the information given in OP. I modified the OP. But if they could overlap, the answer would be infinity, so not much of a problem. Edited December 12, 2008 by xucam Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 I modified the OP. But if they could overlap, the answer would be infinity, so not much of a problem. In that case 50 Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 (edited) 36 Edited December 12, 2008 by Llam4 Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 How is that proof? You just assumed the square was 10x10. Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 How is that proof? You just assumed the square was 10x10. it doesn't matter if it's 10X10 or not, the key is the 2:1 scale of the rectangle. No matter what the dimensions of the square, the answer will always be 50. Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 (edited) it doesn't matter if it's 10X10 or not, the key is the 2:1 scale of the rectangle. No matter what the dimensions of the square, the answer will always be 50. You're still just assuming that k = 10x... k is one of the sides of the square, x is the short side of the rectangle. Edited December 12, 2008 by Llam4 Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 it doesn't matter if it's 10X10 or not, the key is the 2:1 scale of the rectangle. No matter what the dimensions of the square, the answer will always be 50. Not exactly, what if you had a 1x2 unit rectangle in a 400x400 square? The drawing is not necessarily to scale, so no fair measuring and counting. Use the circle, Luke. BTW, how the heck do you get your attachment into the spoiler box? I see the markup, but how did you figure out that the images was 1419:part3.jpg? Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 You're still just assuming that k = 10x... That's my point, with the given relations, k must = 10x. Otherwise the circle is not tangent to the square on all 4 sides. Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 Not exactly, what if you had a 1x2 unit rectangle in a 400x400 square? The drawing is not necessarily to scale, so no fair measuring and counting. Use the circle, Luke. BTW, how the heck do you get your attachment into the spoiler box? I see the markup, but how did you figure out that the images was 1419:part3.jpg? Then the corner of the 1 x 2 rectangle wouldn't touch the circle. The scale is 1:2 not the units. After you insert the attachment, cut and paste the code into the spoiler. Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 That's my point, with the given relations, k must = 10x. Otherwise the circle is not tangent to the square on all 4 sides. In that case, you posted your answer, not the proof. The proof would be the math proving that 10x = k. Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 Then the corner of the 1 x 2 rectangle wouldn't touch the circle. The scale is 1:2 not the units. After you insert the attachment, cut and paste the code into the spoiler. Can you show with a formula or diagram why the proportions must be as you say in order for the rectangle to touch the circle? And thanks for the tip. Quote Link to comment Share on other sites More sharing options...
0 bonanova Posted December 12, 2008 Report Share Posted December 12, 2008 Scale doesn't matter, so let radius be unity. Equation of circle is [1-x]2 + [1-y]2 = 1 substitute x=2y to get 5y2 - 6y + 1 = 0 y = [6 +/- sqrt(36-20)]/10 y = 1 or .2 the first solution is the right side point of tangency. Use the second. y = .2 x = .4 xy = .08 area of square = 4 4/.08 = 50 Quote Link to comment Share on other sites More sharing options...
0 dms172 Posted December 12, 2008 Report Share Posted December 12, 2008 i look a the general sizes in the picture and it looks 5X10 0r 50 Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 (edited) Scale doesn't matter, so let radius be unity. Equation of circle is [1-x]2 + [1-y]2 = 1 substitute x=2y to get 5y2 - 6y + 1 = 0 y = [6 +/- sqrt(36-20)]/10 y = 1 or .2 the first solution is the right side point of tangency. Use the second. y = .2 x = .4 xy = .08 area of square = 4 4/.08 = 50 Hokie got the right answer first, although he wouldn't share the details. Bonanova has solved it here, using a different approach than I had imagined - but got to the same point. Here I've shown a triangle in order to equate the radius and the side length x. AT = r = radius TB = r - 2x AB = r - x This is a right triangle, so Pythagorus can tell you how to solve, and it turns out that r is 5x, the rest is simple math. Or you can say that it is a 3-4-5 right triangle and cut out the factoring. Edited December 12, 2008 by xucam Quote Link to comment Share on other sites More sharing options...
0 Guest Posted December 12, 2008 Report Share Posted December 12, 2008 (edited) Hokie got the right answer first, although he wouldn't share the details. Bonanova has solved it here, using a different approach than I had imagined - but got to the same point. Here I've shown a triangle in order to equate the radius and the side length x. AT = r = radius TB = r - 2x AB = r - x This is a right triangle, so Pythagorus can tell you how to solve, and it turns out that r is 5x, the rest is simple math. Or you can say that it is a 3-4-5 right triangle and cut out the factoring. Sorry I was working on my method and got busy, (pesky work) <_< but it is essentially the same principle. I just put the 2x:x rectangle in all 3 corners and connected the dots of 3 to get a right triangle using the diameter as the hypotenuse. This gives((diameter-2x)^2 + (diameter-4x)^2)^1/2=diameter which works out to diameter = 10x which I so arrogantly stated earlier with no proof only pictures. My fault, I'll word the proof before I draw the picture next time. I must say, Bonanova, your solution is quite elegant and one I didn't see at all even though the principles are the same. Credit goes to Bonanova on this one, he got the proof up before me!! Edited December 12, 2008 by HokieKen Quote Link to comment Share on other sites More sharing options...
Question
Guest
The circle C is inscribed in the square S, i.e. they intersect at points i,j,k,l.
The rectangle R has sides of length x and 2x, has one corner in common with S, and touches C at point T.
How many such rectangles can fit inside the square?
[Edit]
How many *non-overlapping* rectangles the size of R can fit in an *empty* square the size of S.
[/Edit]
Edited by xucamLink to comment
Share on other sites
19 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.