3 pairs of tiles. Each pair identical, 3 pairs different. Keeping the 3x2 layout shown, assuming the tile positions can be individually swapped and individually turned by 180 degrees, how many combinations are there?
Extention: How many combinations if there were 6 unique tiles?
Question
Mortimer
3 pairs of tiles. Each pair identical, 3 pairs different. Keeping the 3x2 layout shown, assuming the tile positions can be individually swapped and individually turned by 180 degrees, how many combinations are there?
Extention: How many combinations if there were 6 unique tiles?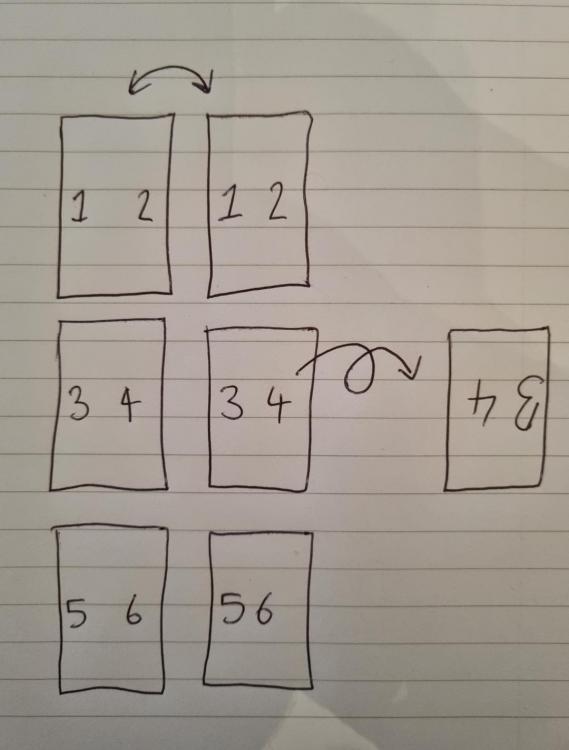
Link to comment
Share on other sites
1 answer to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.