A sphere of radius R=1 sits on the x-y plane at its origin. A second sphere of radius r<<1 is balanced on top of the first. That is, their centers are at [0, 0, 1] and [0, 0, 2+r] respectively. The surfaces are frictionless.
A butterfly in the Amazon Forest imparts to the top sphere the slightest of horizontal velocities, causing it to slide downward along the surface of the bottom sphere. At one point the spheres break contact. At a later point the smaller sphere lands on the x-y plane.
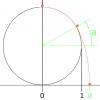
At what north latitude on the bottom sphere do they break contact? That is, how many degrees a above the bottom sphere's equator.
At what distance d from the origin does the smaller sphere land on the plane?
Question
bonanova
A sphere of radius R=1 sits on the x-y plane at its origin. A second sphere of radius r<<1 is balanced on top of the first. That is, their centers are at [0, 0, 1] and [0, 0, 2+r] respectively. The surfaces are frictionless.
A butterfly in the Amazon Forest imparts to the top sphere the slightest of horizontal velocities, causing it to slide downward along the surface of the bottom sphere. At one point the spheres break contact. At a later point the smaller sphere lands on the x-y plane.
That is, how many degrees a above the bottom sphere's equator.
Edited by bonanovaAdd figure
Link to comment
Share on other sites
4 answers to this question
Recommended Posts
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.