-
Posts
871 -
Joined
-
Last visited
-
Days Won
7
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by Prime
-
-
I read this one long time ago in Russian translation of one of Martin Gardner's books.
One of the conditions there is that the Judge cannot possibly lie. It is an old, very interesting twist on liars' paradox. I believe the mostly accepted solution is:
The proposition made by the judge is not decidable. Therefore, the condemned man may not derive any inferences from it. They could execute him on the very last day Saturday, and still it would be a surprize. Thus it turns out, the judge did not lie.
-
You have a dozen (12) stones weighing a whole number of grams between 1 and 6 each. You can obtain one reference weight of your choosing.
What reference weight can you choose to be able to figure out the individual weights of the 12 stones using a balance device for any possibility that may exist therein?
For an encore: what is the maximum weight range of stones (1 to N) that you could solve using 2 reference weights of your choice? Provided you can have as many stones as you need.
I don't believe, I have solved this one myself. We could make it a community project after the first question is answered.
HISTORICAL NOTE:
This problem originated on Brain Den. I constructed it based on Bonanova's problem Weighty Thoughts: http://brainden.com/forum/index.php/topic/4932--/?p=84107 few years ago.
Back then limited number of people participated. The solution found was for specific numbers in that problem (range 1 to 5) – not general. I'd like to give it another try.
-
Assuming a zombie is an average person, he/she encounters 13 other persons a day converting 6.5 of them into zombuism.
It would be a simple geometric series, except as the number of zombies grows, more and more of them encounter each other. -
Another way of tackling the problem requires challenging the wording of the puzzle. Nothing in the wording specifies the formation of the circle. I.e., are the circles DISCS or RINGS? Answers provided thus far assume the circles are to be shaped as discs. But if they can be rings, then only one sheet of paper is needed.
If the "circles" can be rings, here's how it can be done with one sheet of paper. Rather obvious but I like to spell things out anyway:
Position one sheet of paper in the "portrait" orientation and cut it into horizontal strips (at least 20). The circumfance of a 2.5" radius circle is 15.7". So working with the 20 strips of paper each 8.5" long, you'll need two strips to form a ring 5" in diamter. Its a simple matter to tape two strips together on both ends to form a 5" diameter ring... err, circle.
I thought about that. But the OP states your child needs to "cut out 10 circles". Her assignment was not to "glue," "tape," "construct," or even "make" -- it was "cut out."
Although, she should still get her credit and praise for creativity, if she does not blab out that a parent has done the project for her.
-
If I understood the statement of the problem right:
1). The hour hand changes its state from stopped to moving clockwise, or from moving to stopped every time the minute hand passes over it.
2). The minute hand continues moving in the same direction as before when it passes over the moving hour hand and reverses its direction when it passes over the stopped hour hand.
The full cycle is:
(12/11 + 12/13 +2) hours.To get to an exact hour mark that cycle must be multiplied 11*13=143 times
(12/11 + 12/13 +2)*143=574
Now 574 has a remainder of 10 when divided by 12. Or it can be viewed as remainder = -2.
Thus it takes 6 of those "exact hour" cycles to get to 12:
574*6=3444.
Remembering that on the last hour of the cycle the minute hand is making a backward circle while the hour hand stays put, thus repeating the same time:
3444 - 1 = 3443 hours. After that much time the hour and the minute hands will meet at 12.
There is another possibility for intermittent exact hour mark meetings.
Let the clock run to its first stop at 12/11 hours, then start adding full cycles. This way we need a multiple of 13 full cycles where we may run into an exact hour mark meeting. Playing with modular arithmetic we find that starting at 12/11 after 65 cycles an exact hour mark meeting will occur:
12/11 + (12/11 + 12/13 +2)*65 = 262.
That again gives the remainder of 10 (-2) when divided by 12 and we need 6 of those big cycles to get to the 12-hour mark:
262*6 = 1572 hours. When the hour and minute hand meet at 12 again.
Here during the last round of the last cycle the hour hand is moving, so we may not subtract an hour. Still it is less than 3443, so that should be the answer. There is no point in trying to mix the 574 and 262- hour cycles since they have the same remainder from the division by 12.
1572 hours.
-
Then the problem is solved tor a straght line escape and it is the tangential line off the inner circle's perimeter. The new problem becomes how to feed the Ogre. Perhaps, if we convinced the maiden that there is such a thing as zig-zag mode, the Ogre could get his dinner after all.
The function of the Ogre/Maiden rate looks like this (unless I messed something up again):
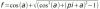
Where a is the angle on Bonanova's diagram. The function increases continuously within its domain from a = o (nearest point escape) to the tangential line escape. The tangential line is the limit, after which the function is no longer valid, because the Ogre changes his direction. The angle a corresponding to the point where the tangential escape goes is approximately 77.5 degrees. The rate of speeds Ogre:Maiden f ~ 4.6033
One thing that seems obvious to me is the Ogre's strategy. At each instant, he spots the point on the shore nearest to the boat and runs there along the shorter arch. The optimal path for the maiden is fixed. Whenever she starts zig-zagging wandering off that path, she must start over, or end up as a main course at Ogre's dinner table. The best (and necessary) headstart for the maiden is where she is on the perimeter of her circle r=R/f and the Ogre is on the opposite end of the straight line drawn from the boat through the center of the lake. If the maiden wanders back inside her inner circle r, she loses her headstart advantage and must work to get it back.
The Ogre can determine the spot on the shore nearest the boat by drawing a straight line from the center of the lake through the boat to the shore.
Although, the straight line escape, most likely is not the optimum. The optimum must be some curve dictated by Ogre's movement. To prove (or disprove) that we could let her row half way along the tangent line and then figure out new optimal path from that position.
-
...
Edit:
We can't continue indefinitely increasing the angle however.
At some point it will become to the ogre's advantage to reverse his direction.
For a straight line escape, it seems clear that the optimal angle is between the zero (straight line to the nearest point on the shore) and the tangential line escape. Past the tangential escape, maiden re-enters her inner circle going towards the Ogre causing him to change the direction.
You have calculated the precise rate O:M rate (f) for the tangential escape. And it is better than the nearest point escape.
However, for the other angles in between those two, calculation of maiden's trip is a bit more messy.
I think this problem still has a suspense left and warrants further investigation.
-
so you mean the Ogre looks South, and the Maiden takes off to the North, and the Ogre (a Zen master apparently) sees the inevitability, and continues the long way around, like Mark Twain's "Cooper Indian". If the Ogre does turn and go north, he can go four times further north than M can. Exactly when should M recalculate her new tangent? Will it really require as long a road for Ogre?
It is a lot simpler than that for the zen master Ogre. The Ogre ignores where the maiden looks, where she goes, and where she intends to go. Ogre simply draws an imaginary straight line from the center of the lake, through the boat, to the shore; and heads for that spot using the shorter arch. Insofar as the optimum is concerned, it is the Ogre who determines the path -- not the maiden. The maiden reacts to Ogre's moves, not other way around.
If the maiden wanders back into her inner circle r, that could make the Ogre change the direction when the boat crosses straight line drawn from the Ogre to the center of the lake. Then the young lady would be going towards Ogre rather than away from him. (Not an optimal strategy.)
Presently, we are solving the sub-problem, where the maiden after leaving her inner circle goes in a straight line towards some point on the shore. We must find, that point. Bonanova suggested going off the inner circle on a tangent line. That gives a better ratio than going in a straight line to the nearest point on the shore. However, I don't believe it is the optimum.
The numbers I have given in the post #23 inside the spoiler are off. But then, as everyone knows, I am siding with Ogre.
Blame it on the cold, Prime.

I am not convinced that tangential is optimal - it may not be enough!
It's easy to overlook that r is one of the unknowns.
I did overlook that r is one of the unknowns because of cold and my partiality to Ogre's cause.
Still I don't see that the problem is solved even for a straight line escape.
By the way, I did not see the answer by Phaze to which you referred. Is BD not displaying some of the posts to me?
-
so you mean the Ogre looks South, and the Maiden takes off to the North, and the Ogre (a Zen master apparently) sees the inevitability, and continues the long way around, like Mark Twain's "Cooper Indian". If the Ogre does turn and go north, he can go four times further north than M can. Exactly when should M recalculate her new tangent? Will it really require as long a road for Ogre?
It is a lot simpler than that for the zen master Ogre. The Ogre ignores where the maiden looks, where she goes, and where she intends to go. Ogre simply draws an imaginary straight line from the center of the lake, through the boat, to the shore; and heads for that spot using the shorter arch. Insofar as the optimum is concerned, it is the Ogre who determines the path -- not the maiden. The maiden reacts to Ogre's moves, not other way around.
If the maiden wanders back into her inner circle r, that could make the Ogre change the direction when the boat crosses straight line drawn from the Ogre to the center of the lake. Then the young lady would be going towards Ogre rather than away from him. (Not an optimal strategy.)
Presently, we are solving the sub-problem, where the maiden after leaving her inner circle goes in a straight line towards some point on the shore. We must find, that point. Bonanova suggested going off the inner circle on a tangent line. That gives a better ratio than going in a straight line to the nearest point on the shore. However, I don't believe it is the optimum.
The numbers I have given in the post #23 inside the spoiler are off. But then, as everyone knows, I am siding with Ogre.
-
Phaze has got the answer, at least as far as I have analyzed it.
That being true, I will post my analysis and people can take pot shots at improving it.
The large circle, radius R, is the lake. The smaller circle, radius r, contains the escape starting point for the boat. The ogre's speed multiple is f > 1, so R = f.r, using the period to mean multiplication. The rower has thus achieved her greatest possible separation from the ogre for which she can maintain the lake's center directly between them. We now compare two escape strategies.
[1] Radial escape.
The three black dots are, from right to left, the Ogre's and the rower's starting points, and the point on the shore that each heads for as the chase begins. The black circular arc is the ogre's path, and the black leftward arrow is the rower's path. The equation of simultaneous arrival is simply
f.x = R.pi = f.r.pi
x = r.pi
Noting that x = R-r = r(f-1) we obtain
f = 1 + pi = 4.14159...
as the maximum ogre speed factor advantage that can be overcome using radial escape.
She must be able to row 0.966 mph.
[2] Tangential escape.
The red dot now is the point on the shore that each is headed for. The sum of the black and red circular arcs is the ogre's new path, and the red upward arrow is the rower's new path. The equation of simultaneous arrival is a little more complicated, but not much.
First, we need to find the extra path length for the ogre. It's simply a.R [the red arc] where a is the angle from horizontal to the new destination point. Thus
f.y = R(pi + a) = f.r(pi + a)
y = r(pi + a)
Noting that tan(a) = y/r
tan(a) = pi + a which gives a = 77.45 degrees.
Noting that cos(a) = y/R = 1/f, we obtain f = 1/cos(77.45)
f = 4.6033
This is an 11% increase in the ogre's speed that can be overcome using tangential escape compared to radial escape.
Thus the rower can row 11% slower and still escape.
She need only row 0.869 mph.
--------
Two comments.
First, this is also only a sufficient condition. This analysis does not rule out a more efficient escape strategy. Spirals are good next steps to investigate. Piecewise linear escape paths would be easier to investigate.
Second, one could ask whether the ogre, once he sees the direction taken by the rower, might not help himself by switching directions and taking the shorter route to the red dot. The answer is no. If he does, the rower fires up photoshop, constructs a new, larger inner circle, and heads tangentially for shore in the other direction, the result of which is actually to the rower's net advantage. The ogre's best strategy is to stay the course [clockwise in this case] for the red dot.
The drawing is for a value of f in the general range we are considering. That is, a is not exact, but close to 77.45 degrees. Thus it is valid to perceive the advantage of tangential escape by noting that y is not significantly larger than x, while a + pi is significantly larger than pi. Tangential escape makes the ogre's task more difficult.
Tangential escape does not seem the optimal even for the straight line escapes. The straight line escape with a 45-degree angle seems to perform better.
-
I have a cold, my head is stuffed, I feel like an Ogre. I am not figuring out the differential equations to deny hungry Ogre his meal. However, here is some food for thought for those Brain Denizens who took the maiden's side. Indeed, she could go slower. Mayhap, someone will try carrying out the required calculations, make an error and give the maiden a wrong advice.
To make the contest fair, the maiden should have only so much time for rowing. Having exhausted it, she falls asleep. Whereafter, the Ogre should start blowing at the boat pushing it towards the shore...
-
-
I was developing a winning strategy for the Ogre based on the inertia of the boat. But then Bonanova added an infinite acceleration.
Once outside her small circle perimeter, maiden can no longer keep the center of the lake between herself and Ogre. However, she could point the nose of her boat to the point opposite Ogre. As long as she still approaches the shore. Would that help?
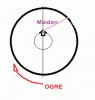
If maiden went at an angle, would she increase her distance at lesser rate than Ogre's?
What if maiden zig-zagged her boat pointing to the left and right of the point on the shore opposite to the Ogre's position? I hope the Ogre is smart enough to ignore the direction where maiden goes and head to the point on the shore closest to her boat.
Either way, the Ogre is at disadvantage. Whenever maiden feels she is not making it, she could always turn back to the center of the lake. Ogre should try and woe her instead of chasing.
-
Once she is off her small cirle making her dash for the shore, and the Ogre chose his direction; she could continue spiraling away. Would it buy her an additional advantage? How well versed are Ogres in Calculus?
-
I would recommend the maiden should first find the radius r where she could circle in the same time it takes the Ogre to run around the entire lake of the radius R. She must do so while keeping the center of the lake between herself and the Ogre in a straight line. Once she has achieved that, she should make a dash for the shore in a straight line of the length R - r. While the Ogre will have to run around half the lake (Pi*R) distance to catch her.
If the speed of the maiden is M and the Ogre - O, then
1). Pi*R/O = Pi*r/M; ==> r = M*R/O; (equation for the circle)
2). (R-r)/M = Pi*R/O (equation for the dash.)
Solving for the M, we get: M = O/(Pi + 1);
If she cannot row faster, she must use her cell phone to call Ogre Protection Agency.
Nice problem.
Are you sure she has to row that fast?
The question in the OP is: "How fast she must she be able to row..." (meaning top speed.)
Her average speed could be less. She could take time getting onto the perimeter of the small circle. However, once there,
R - r distance for maiden vs. Pi*R for Ogre seems to be the optimal.Her speed has to be ~ 4/4.14 mph. I'd say I mph to maintain some distance. (Ogres have long hands.)Alternatively, maiden coulld make smaller circles while the Ogre runs all the way around the lake, until he drops from exhaustion.
-
The series is infinite, and the variable term thus equals zero. There are equal numbers of boys and girls on average. Bonanova is right. It's a happy ending. In each generation everyone gets his/her mate.

-
I would recommend the maiden should first find the radius r where she could circle in the same time it takes the Ogre to run around the entire lake of the radius R. She must do so while keeping the center of the lake between herself and the Ogre in a straight line. Once she has achieved that, she should make a dash for the shore in a straight line of the length R - r. While the Ogre will have to run around half the lake (Pi*R) distance to catch her.
If the speed of the maiden is M and the Ogre - O, then
1). Pi*R/O = Pi*r/M; ==> r = M*R/O; (equation for the circle)
2). (R-r)/M = Pi*R/O (equation for the dash.)
Solving for the M, we get: M = O/(Pi + 1);
If she cannot row faster, she must use her cell phone to call Ogre Protection Agency.
Nice problem.
-
The proportion is roughly the same, but not exactly. Since there are only
n married couples (where n happened to be a power of 2,) the following marriage procedure must be instituted.
First, the girls who have no brothers (1/2 of the families) pick one boy each from the remainnig half of the families. Then 1/4 of the girls whose only brother was taken pick their husband from the other 1/4 of the families. That leaves 1/8 of the families where all boys were taken.
And so the procedure of choosing mate must continue. In the end, one girl would remain without a match. She must go to war abroad. The number of couples in the next generation would decrease by 1.The above procedure for choosing mate may be a hint at how to construct a closed-form expression for the series.
-
Oops, seems I messed up again.
The result of the series for the average number of boys per family should be:
1 - (n+1)/2n+1
Send extra girls to war. -
The number of people in the society is not specified either. I assume, there are n married couples.
There is exactly one girl per each family. I estimate the average number of boys per family is:
1 + 1/2n * (n - 1/2).
So, just a bit more boys than girls. When they reach marrying age, I say, send the extra boys to war abroad. Make sure all the rest are married and procreate in the prescribed fashion to maintain the population. -
To reiterate the point Bushindo has made already (post#4.)
There is a difference in average distance from origin after n steps and how many steps are required on average to travel that far. The average distance includes variations where the drunkard has traveled further and then returned. On the other hand, to travel further than 1.5 steps, he must make at least 2 steps. The probability of leaving the area after one step is zero, so the first step does not add anything to the average steps; whereas it does add its full size to the average distance.
One way to run a computer simulation is to make random steps until the drunkard wanders past the designated radius, tally up the steps it took for each experiment and calculate the average. That should show how many steps it takes on average to leave the area.
Another way is to have n steps in each experiment, tally up the distances traveled, calculate the average. That would show the mean distance from origin after n steps.
-
Oops, forgot another square root. Here is the correction/addition to the previous post.
Normally, I try to avoid using integrals and calculus in general. I don't like that branch of mathematics and don't believe in it.
So it is entirely possible I messed up the above formulas. Besides, I have not actually figured out the Integral I used for this solution. But never mind all that. I checked few sources on the internet regarding two-dimensional random walk problem. I did not feel like submerging into the complex math presented there. Imo, those sources used insufficient justification and explanation for the formulas they use. What's interesting, in my brief examination, I did not see my concept of the average increase in distance from any given point with each step in the treatments of Random Walk in Two Dimensions. (As shown on the diagram in my previous post.)
Are there any professional mathematicians here to shed light on this?
-
I believe this problem is about a drunk man, not an ant. He takes 1 meter step, falls, gets up makes another step in random direction, and so on.
If there is no directional bias, and that applies to both orientation and size of the step, then we expect the excursions of the ant to average out to zero. In fact, the probability in both one and two dimensions is unity that the ant will come back again [and again] to his starting point.
But between these visits to his origins the ant will wander away in one direction or another, and after any particular number of steps, he will be some expected distance away from his starting point. We would expect this distance to increase, but not necessarily in a linear fashion, with the number of steps taken.
The way we calculate this expected travel distance is to average a quantity that is always positive. That quantity is the square of the distance. Let's assume, just to explain how this works, that the ant travels in one dimension, along the x-axis; his steps are of length |s|, where s is the individual step vector, which may or may not be constant for each step; and that left and right motions are equally probable.
Again, if we consider the distance itself, equaling the sum of N random (vector) excursions to the left or right with equal probability, that average will tend to zero. That's just what we mean by unbiased. But if we average the square of the distance after N steps, we get a slew of product terms to find the average of. The product terms are of two types: [1] the squares of the individual step distances and [2] all the pairwise products of two different step vectors. The first type are always positive. Those of the second type are either positive or negative, in equal numbers, and they cancel out.
Thus, if dN = s1 + s2 + s3 + ... + sN is the (vector) distance the ant has traveled after N steps,
Then the averages of that distance, and of its square, are,- <dN> = <s1> + <s2> + <s3> + ... + <sN> = 0 + 0 + 0 + ... + 0 = 0.
- <dN2> = <s12> + <s22> + <s32> + ... <sN2> = <s2> + <s2> +<s2> + ... + <s2>
= N<s2>, if s varies from step to step.
= N|s|, if |s| is constant.
= N, if |s| = 1.
That gives us the root-mean-squared [RMS] traveled distance.
dRMS = sqrt(<dN2>) = sqrt(N<s2>)
In the present example, |s| = sqrt(<s2>) is constant and = 1.
dRMS = sqrt(<dN2>) = sqrt(N)
This is the desired formula.
The ant will have traveled an expected distance dRMS = 3 after taking 32 = 9 steps.
It may not seem intuitive, but this result also applies in two and three dimensions.
-------------------
Edit: Rereading the OP, I see the diameter is 3 meters.
So the ant has to travel 1.5 meters. This will take on average 2.25 steps.
Or maybe you meant radius of 3 meters..I don't see how this trip averages out to zero and returns to the same point. Clearly, it is not true for the first step. And the probatillity of getting back to the point of origin on the second step is slight.
I am not sure wheter the title I used "Two Dimensional Random Walk" is the conventional name for this problem. Must check the literature, (which I never do.)
- <dN> = <s1> + <s2> + <s3> + ... + <sN> = 0 + 0 + 0 + ... + 0 = 0.
-
I found this interesting 102-digit number: 490000...000077 (“49”, followed by 98 zeros, followed by “77”.) If you multiply that number by 111...111 (one hundred 1-s), the resulting 201-digit number:
54444...4447555...55547 (“5”, followed by 99 “4-s”, followed by “7”, followed by 98 “5-s”, followed by “47”) meets the conditions set forth in the OP, except I cannot guaranty it is the smallest number that does. (I did not find any simple combination of "1-s" and "0-s", which multiplied by all "7-s" would yeild "4-s", "5-s", and "7-s", while avoiding "8-s".)
On a side note. While playing with these numbers I found a simple yet curious divisibility rule, of which I was not aware before. I should try and construct a problem based on it.





Weighing Problem Resurected
in New Logic/Math Puzzles
Posted
There is no guaranty what weights are present/absent in your collection. The only guaranty is that each of the stones weighs a whole number of grams between 1 and 6.
12 stones each weighing 6 grams is one of the variations we must account for.