-
Posts
871 -
Joined
-
Last visited
-
Days Won
7
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by Prime
-
-
Timmy is much older and thus more physically mature than James.
The key phrase, "one day" means sometime in the future but since we do not know how far in the future 'one day' is, it is perfectly plausible to assume that 'one day' occurred many years later and thus Timmy is now a young college student sitting by himself on a dune when three butt head 8th graders come over to bother him.
The grammar in the OP contradicts that solution.
Then again, what do I know. English is not my native language.
-
Possibly, you have found the smallest number fitting the conditions in the OP. However, a simple proof/solution does not present itself. When designing new puzzles that comes with the territory.
I appreciate invention of new puzzles. It's a different process from uncovering an answer that has been found before. While playing with this problem I came up with some interesting divisibility rules, which could be used to construct riddles, or break public/private key encryption.
Perhaps, this particular puzzle could be simplified by requiring two digits in the product, rather than three.
The point of giving large numbers, like 100 7s, is to force analytical solution, rather than heuristic approach with actual multiplication or division. Let's construct a number consisting of just 5s and 7s, which is divisible by 100 7s.
First, we note that all 7s divided by 7 yields all 1s, which may be easier to work with. Although, we add a new restriction: multiplier must be divisible by 7.
When multiplying 111...111 by a number, the digits of the product are going to be sums of the digits of the multiplier plus carry, if any. For example, take 525 as a multiplier. The rightmost digit of the product is 5, next one is 5+2=7, after that 5+2+5 resulting in 2, then digit 3 will be repeated: 5+2+5+carry(1). At the left edge, the first 5 will drop out resulting in 5+2+carry(1) = 8, then 2 goes away, leaving 5 as the leftmost digit of the product.
However, we want only 5 and 7 as our product digits. If we carry the leftmost 5 outside 100th digit perimeter putting zeros in the middle, the rightmost 5 shall drop out when the leftmost 5 kicks in. That is, 100 1s multiplied by 101-digit multiplier 5000....00025 will result in 5 on the left and right with a whole bunch of 7s in the middle. Unfortunately, 101-digit number 5000...00025 is not exactly divisible by 7 (yields the remainder of 1.)
Building a number divisible by 7 is an interesting task in itself.
Note the sequence of remainders, the powers of 10 yield when divided by 7:
100 ≡ 1 (mod 7)
101 ≡ 3 (mod 7)
102 ≡ 2 (mod 7)
103 ≡ 6 (mod 7)
104 ≡ 4 (mod 7)
105 ≡ 5 (mod 7)
That sequence of six remainders (1,3,2,6,4,5) is periodic. Curiously, pairs of remainders at the intervals of 3 add up to 7: 1+6=3+4=2+5=7. That leads to many marvelous divisibility rules. E.g., any number with same digits at intervals of 3 is divisible by 7, like 532,532.
So let's build a 101-digit number of the form 500...00200...005, which is divisible by 7. We designate the positions in the large number as 012345,012345,... from right to left. Thus the rightmost 5 is in the position 0 and the leftmost 5 is in the position 5, since 101 ≡ 5 (mod 6). The two 5s add up to the remainder 5*1+5*5=30, or remainder of 2 from division by 7. Now, if place digit 2 in the position 3, we add 2*6=12 to the remainder of 2 for a total of 14, which is divisible by 7.
Thus, 101-digit number 500...002005 is divisible by 7 and when multiplied by 100 1s will result in 3 5s on the right, followed by a whole bunch of 7s, and a bunch of 5s on the left.
Now I want to go back to the sequences of remainders from division of powers of 10 by some prime number greater than 5. Those sequences seem to be a kin to the Little Fermat's Theorem.
Number 13 gives a similar sequence, also of a period 6: (1,10,9,12,3,4). Again, pairs of remainders at interval of 3 add up to 13. And so we know, that a number like 532,532 is divisible by 13 in addition to being divisible by 7. For similar reasons that number is divisible by 11, which has its periodic sequence of length 2: (1,10). However, the fact that 532,532 is also divisible by 19 is purely coincidental.
After a quick study of some other prime number periodic sequences, I can come up with some examples, like 227,772 is divisible by 37. Periodic sequence for 37 being: (1,10,26).
Using those sequences one could come up with a multitude of number tricks.
Since we have been running out of the unproved theorems in Number Theory of late, let me introduce this conjecture:
Prove (disprove) that for any prime number P > 5 as described above, its periodic sequence of remainders is a multiple of P. -
Assuming rows are straight lines, no two different rows may share two trees. Since a row consists of at least 3 trees, there are
3C2 = 3 combinations of tree pairs in each row.
Thus for 19 rows we need at least 19*3 = 57 pairs of trees. The minimum number that allows for that many is 12 trees. (12C2 = 66.)
A tree shares a row with other two trees. It cannot share another row with any of those two trees. If maximum rows in which a tree is a participant is x and total number of trees is N,then 2x + 1 = N. Solving for N=12, x=5.5.
Since no fractional trees are allowed, each tree can participate in at the most 5 rows. 12*5 = 60. However, since each row has 3 trees, 60/3 = 20.
And so it appears a gardener could construct 20 rows with 12 trees.
Now all gardener has left to do is to use these limits as a guide for planting his garden. -
Going with the following assumptions as answers to my questions:
1. Leading zeros are allowed.
2. We work with the sum of numbers, not digits.
3. The school No. 7 is in Moscow in the vicinity of MSU (МГУ) and Vernadski Prospect.
Let's call the first 3 digits of a 6-digit number
h and the last 3 digts t. Then the 6-digit number is 1000*h + t.Let's construct another number by swapping heads and tails, that is putting t up front and h in the back. Thus the swapped number is 1000*t + h. Clearly, if the ht is a “lucky number” then so is th. Let's add them together:
1000h + t + 1000t + h = 1001(h+t).
Each 6-digit number has exactly one corresponding swapped number. Some numbers equal to their swapped number. Example: 532,532. Such symmetrical lucky numbers are obtained by multiplying any 3-digit number by 1001: 532*1001 = 532,532.
Thus the set all lucky numbers may be presented as a set of all symmetrical numbers, which are divisible by 1001 and a set of pairs of swapped numbers, where the sum of each pair is also divisible by 1001.
1001 = 7*11*13.
Q.E.D.
I have a different proof of the same, which gives even more insight into divisibility rules, but it would take longer to explain.
We have another Divisibility puzzle going here: http://brainden.com/forum/index.php/topic/15583-more-divisibility/?p=328196]More divisibility
-
Do tickets include numbers with leading zeros?
Do you add together all actual 6-digit numbers, or just the digits from those numbers?
In which town math school No. 7 is located?
Will you also find that the sum is divisible by 7 and 11?
-
Indeed, this number is a bit smaller than the one I found.
Perhaps, it is easier to evaluate as 410000...000214: "41", 97 zeros, and "214" (which is, clearly, divisible by 7) multiplied by 100 "1"s.
But where is the proof that it is the smallest number that meets the conditions?
-
The goat in the picture is about 50 yards long and 40 yards tall. I would not like to meet it in a dark alley.
For any rope length, a field could be built, such that the goat would have access to half of it. I guess, we are looking for the minimum size field.
The minimum rope should allow the goat to reach around half of the silo. Thus the rope length is 29π yards.
After that, it seems, the problem requires solving an integral. -
If "...the weight of the weight and the weight of the rope were together half as much again as the weight of the monkey," how can that system be in equilibrium?
Конечно ...

Веревка подбежал шкив, на одном конце была обезьяна, на другом конце вес.Два оставшихся в равновесии.Вес каната было 4 унции / футбол, а в возрасте от обезьяны и мать обезьяны составил четыре года.Вес обезьяна была много фунтов, как мать обезьяны было лет, и весом весом и весом каната вместе были в полтора раза больше, поскольку вес обезьян.
Вес вес превышал вес веревки, как многие фунтов, как обезьяна лет, когда мать обезьяны был вдвое старше брата обезьяны было, когда мать обезьяны был вдвое старше брата обезьяна будет, когда брат обезьяны в три раза стара, как мать обезьяны Когда мама была обезьяна была в три раза стара, как обезьяна в пункте 1.
Мать обезьяны был вдвое старше обезьяна Когда мать обезьяны был наполовину стара, как обезьяна будет Когда обезьяна в три раза стара, как мать обезьяны было, когда мать обезьяны в три раза стара, как обезьяна в пункте 1.
Возраст матери обезьяны превысил возраст брата обезьяны на такую же сумму, как возраст брата обезьяны превысил возраст обезьяны.
Какова была длина веревки?



So the rope has legs and plays footbal?! And monkey's mother is a male?! And age is money?!
Was it Google translation? I guess, it'll be awhile before computers can understand and translate natural language.
Although it's worth noting that about the only bit translated correctly, is that very thing, which I misunderstood. The translation states, the weight of the rope together with the weight is 1.5 times the weight of the monkey, as the problem statement intended. Whereas I understood it as half weight of the monkey.
-
James must lift first. Thereafter, Timmy must move the contest into the water. If James was not all that strong and could not lift 60 lb over his head, Timmy could win the contest at a shoulder deep place. Otherwise, going into deeper waters and diving would be involved. Questionable.
-
Seems inconsistent.
-
If "...the weight of the weight and the weight of the rope were together half as much again as the weight of the monkey," how can that system be in equilibrium?
-
I assume, like in real life, after an introduction two people immediately become fast friends.
Number them from 1 to n and arrange in order.
Divide the line in half (if odd, put the middle man into the top half.) Introduce everone to each other in the top half.
For the bottom half: Introduce 1st man to the n-th man only; 2nd man to the n-th and n-1st; 3rd man -- to top 3, and so on until the bottom half is all taken care of.
This way only the middle two would have same number of friends.Or here is an alternate procedure amounting to the same thing.
Introduce first two men to each other. For each additional man, introduce him to the top half of the introduced men (sorted by number of friends.) When odd number of men introduce, the top half should include an extra man.
This way the introduced field will grow like so:
1 1
2 1 1
3 2 2 1
4 3 2 2 1
5 4 3 3 2 1
and so on. (Each newcomer is marked in red.)
Same thing as k-man actually.
Note, it is impossible for all n people to have different number of friends, since the maximum number of people a person may know is n - 1, and with that, mininimum is 1. So at least two people must have equal number of introductions.
-
That is some serious analysis. I liked the (b – a) angle, but somehow I don't see that it's been successfully used as a proof of the concept.
Fair enough, if you don't see it. I'm not sure what it left undone.
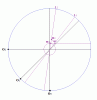
Page 3: “Clearly the blue landing point is advantageous to boat.”
Is the diagram an accurate scale model? If so, the above statement represents a numeric test, not an analytical solution.
Accurate scale:
We both understand that the radius of the inner circle depends on f.
So if you mean exactly the right inner radius, then no. It's approximate.
If you mean are the circles and lines accurately drawn, then yes. They are.
Analytical solution:
My intent is a proof that pi/2 is the optimal bearing.
That is an adequate treatment of the straight-line escape path problem.
Bearing is the only variable.
In a nutshell,
What I showed was that for a straight line escape at any bearing 0 < b < pi/2 it is advantageous to increase b.
That gets us to the maximum allowable b = pi/2 without re-entering the inner circle, and re-starting the race.
Page 4: The angle between brown and black arcs is indeed b – a. However, if you build a triangle with vertexes at the gray and blue points and the intersection of brown arc with blue segment, the corresponding angle seems different, and the triangle is not a right-angled triangle. I can't even decide whether sin(b-a) is greater or smaller than the actual Δp/ΔO ratio.
Of course we are talking about derivatives, not deltas, and tangents, not arcs.
To draw a triangle with infinitesimal sides is not possible.
The blue line is drawn from the center of the brown arc.
A radius is always perpendicular to its circle.
Page 6: I guess, cos(a) = y/R = f is a typo. It should be cos(a) = r/R = 1/f.
Plugging in the value a = 77.445˚ ~ 1.35167 radians, yields f ~ 4.6003.
You are correct, that is a typo.
Also, when I did the analysis I used one definition of f and when I wrote it up I changed to the other.
So an early version of the document was inconsistent on that point.
The version of the document currently attached to the post I believe is consistent.
Throughout, I referred to the boat relative to the Ogre.
So f as the speed ratio is defined to be < unity.
These equations are the ones that use f, and I think they are consistent:
f = sb/so < 1
re = fR
f = 1/(1+pi)
f delta tb/delta to = delta p/delta O .
sin (a-b) = f
y = fR (pi + a) = r (pi + a)
cos (a) = f.
f = 0.24174 = 1/4.6003 - with corrected values.
Now let's do an alternative calculation for f. Using diagram on page 5:
y = R*sin(a), that is the distance traveled by the boat.
The Ogre has traveled (π + a)*R. Thus Ogre:Maiden ratio = (π + a)/sin(a). Plugging in the same value for a, we get f ~ 4.6033, which is drastically different from 4.6003 – life vs. death for the maiden.
(Incidentally, the same result I got from evaluation of my function given inside the spoiler in post #34.)
I don't really know how to solve tan(a) = π + a, but for the purposes of our problem a ~ 77.4534˚ fits the bill better.
You solve it iteratively - Newton's method works.
Actually I think this was another typo - 77.445 instead of 77.455.
But seriously a better solution is 77.453397562356507 deg
That gives the speed ratio as 0.2172336282 = 1/4.603338849
There is another typo, I guess, sin(a-b) = f should be sin(b-a) = 1/f. (f being Ogre/Maiden ratio.) Is that a true formula for the f instead of the one I've given in post #34? Do those formulas amount to the same thing? Note, b and a are dependent variables. a = function(b), or vica versa.
I define f as maiden/ogre speed < 1.
If by true formula you mean accurate, or valid, then yes it is..
As for the “spiral escape paths,” I could not really follow the argument in point (3) and did not see the need for the argument in (2). I believe, the argument in (1) is sufficient. Apparently, I failed to explain clearly my point in the post #39 and the function in the post #34.
I guess it's sufficient to say a straight line to the landing point is optimal.
Statements 2 and 3 were intended simply to put some of the equations into words.
In effect, statement 3 says you want to intersect the shoreline closer to perpendicular than to parallel.
A spiral path does just the opposite.
OK?
So the Ogre and the Maiden problem is actually a solution/approximation method for tan(x) = x + π.
I worked off the initial version of your .doc file (opened it when you made the post, but got around to it couple days later.)
Still, the typo remains: sin(a-b), where you meant sin(b-a) (page 6.) Sorry for nitpicking.
It seems my actual formula for Ogre/Maiden speed rate is being summarily rejected here. I don't see why.
Here is an addendum to put some finer points on your sin(b-a) analysis and to reiterate the actual formula for f:
-
I have finished a rigorous proof that the tangent to the inner circle is the
best path, straight or curved, that permits the girl and boat to reach shore
safely, with the lowest speed ratio compared with ogre, namely 0.2174,
or 1/4.6003.
It shows also that reversing direction is not part of either Ogre's or
the girl's best strategy.
Does it cover all the bases?
Looks like the maiden gets an unfair edge here. The calculated rate does not give the Ogre his chance, unless the lake is really small and Ogre's hands are really long.
That is some serious analysis. I liked the (b – a) angle, but somehow I don't see that it's been successfully used as a proof of the concept.
Page 3: “Clearly the blue landing point is advantageous to boat.”
Is the diagram an accurate scale model? If so, the above statement represents a numeric test, not an analytical solution.
Page 4: The angle between brown and black arcs is indeed b – a. However, if you build a triangle with vertexes at the gray and blue points and the intersection of brown arc with blue segment, the corresponding angle seems different, and the triangle is not a right-angled triangle. I can't even decide whether sin(b-a) is greater or smaller than the actual Δp/ΔO ratio.
Page 6: I guess, cos(a) = y/R = f is a typo. It should be cos(a) = r/R = 1/f.
Plugging in the value a = 77.445˚ ~ 1.35167 radians, yields f ~ 4.6003.
Now let's do an alternative calculation for f. Using diagram on page 5:
y = R*sin(a), that is the distance traveled by the boat.
The Ogre has traveled (π + a)*R. Thus Ogre:Maiden ratio = (π + a)/sin(a). Plugging in the same value for a, we get f ~ 4.6033, which is drastically different from 4.6003 – life vs. death for the maiden.
(Incidentally, the same result I got from evaluation of my function given inside the spoiler in post #34.)
I don't really know how to solve tan(a) = π + a, but for the purposes of our problem a ~ 77.4534˚ fits the bill better.
There is another typo, I guess, sin(a-b) = f should be sin(b-a) = 1/f. (f being Ogre/Maiden ratio.) Is that a true formula for the f instead of the one I've given in post #34? Do those formulas amount to the same thing? Note, b and a are dependent variables. a = function(b), or vica versa.
As for the “spiral escape paths,” I could not really follow the argument in point (3) and did not see the need for the argument in (2). I believe, the argument in (1) is sufficient. Apparently, I failed to explain clearly my point in the post #39 and the function in the post #34.
-
If I read the picture properly, the Ogre can walk all around the lake in 8 steps. I agree that O would be foolish to tack. I was imagining a much larger lake. Sorry to disturb you guys.
I am not disturbed. Your question points to an essential unsolved part of the problem. How should rower recalculate her path if Ogre deviates from optimal.
I used the diagram to explain the idea. The picture is not to scale and very scetchy. I used large steps to make it more illustrative. The size of the lake does not matter, only the ratio of speeds does. The same concept applies if it takes the Ogre thousands of steps to run around the lake.
Anyone can still work on this problem to find more efficient and creative ways for recalculation of rowers path. As well as finding how long it takes to escape, and or how far away the Ogre would end up at the landing.
-
This is a good clear thorough analysis of the tangential escape--a better linear escape than the straight-ahead escape or my wait-until-Ogre-has-committed-22-degrees escape.
I'm sorry to be beating a dead horse, but I would now like to revisit the issue of the tacking duel. In particular, if we suppose that in the very first second of time, Ogre moves CW and Maiden moves at angle a, as determined above. Now suppose that in the next second, Ogre reverses direction ("tacks") and steps back to O's start point, moving CCW.
(1) What is M's move? Does she do that recalculation you mentioned? If so, it's a different calculation, as she is now no longer directly opposite Ogre, and (in a large enough pond) hasn't gotten to a point where she has a guaranteed straightline solution.
(2) If she does not recalculate, I predict the Ogre will continue moving CCW. WHEN will M do her recalculation, and what will it look like then?
I see the makings of a computer game Ogre vs. Maiden.
Since both Ogre and Rower can turn on a dime and have infinite acceleration, any history of their moves means nothing. The Ogre's strategy is to spot the nearest landing point for the boat and run there along the shorter arch.
However, the maiden must be given some small advantage in the speed ratio. Ogre knows that, and he is also aware that the young lady has read our blog and knows all about the optimal path. So the Ogre deviates from his optimal strategy, giving his opponent an additional advantage. But if she is so dumb as to continue on the path she started, she'll run straight into the Ogre's paws.
Suppose, we gave the maiden a small advantage to ensure she has time to jump out of the boat before the Ogre grabs her, say, instead of our calculated 4.6033 factor, the beast can move at his best only 4.5 times faster than the rower.
Let's add another dimension to the game – limit rower's time. After so many game steps, Ogre's wife, a good swimmer, emerges from her underwater cave and grabs the young woman, whereupon the Ogre couple can have a romantic dinner.
Let's work on CaptainEd's suggestion. The wily Ogre deviates from the optimal path and on his second step goes back to the initial position. The maiden has gained some advantage, but she must recalculate her path. Not finding any clear instructions on how to do that, she may be lost.
We need not bother with Ogre's traveled distance – just the angle he has to travel to the nearest boat landing point.
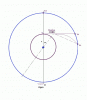
The Ogre made his first step from O0 to O1 . The rower goes from M0 to M1. At this point the Ogre's remaining angle clockwise (O1 to L1 ) is less than π (half circle.) But he goes back to O0 to confuse the young lady. At this juncture, the maiden could draw a line from the Ogre to his opposite point on the shore, then another line to L2 at the same angular difference as it was after the first step, and step onto that line using her top speed. (See the diagram.)
Thus after two steps, the Ogre only has reduced the angular gap the same amount as after the first step. Whereas the maiden is closer to the shore than she was after her first step.
In such way, the rower clearly grabs the advantage afforded by Ogre. Whether the method is optimal for the rower depends on the objective: less steps, or increased distance from Ogre at the landing.
That smallest angular gap may not be maintained on consecutive steps along with advancement to the shore. What we could do is to calculate angular gap for each step in the optimal path and then maintain it in the zig-zag mode. Then the maiden should be able to land while the Ogre would remain pretty much at the opposite side of the lake.
-
Every 60.4195804195804 deg both hands are aligned and cw. If a divider is used, 143 arc steps along the circle will point one of its arms to 360 deg..
I see, I mixed up the adavance of the hour hand with the elapsed time for each cycle. And I calculated period incorrectly for the second part in my previous post.
Still, after the corrections, I get a different answer. My hour and minute hands will meet a lot sooner.
Why rejecting the occurences where the clock hands meet at 12 in a mid-cycle?
I see nothing in the OP prohibiting that. In fact, the clock hands will meet again at 12 on a mid-cycle before they do so after a whole number of cycles.
1.The full cycle is (12/11 + 12/13 +2) = 574/143 hours elapsed time.
The hour hand advances (12/11+12/13) = 288/143 hours
After 143 such cycles, the hour hand advances 288 hours, which is divisible by 12. (288/12 = 24).
Elapsed time after 143 cycles is 574 hours. And, because the last step of the cycle the hour hand stayed put for exaclty one hour, there was a meeting at the same spot one hour prior. Thus after 573 hours from the start the hour and minute hand meet at the 12-hour mark.
2. The hour and minute hands also meet at exact hour mark after 65 full cycles plus 12/11 of an hour. (12/11 + 12/13 + 2)*65 + 12/11 = 132.
It so happens that 132 is also divisible by 12. 132/12 = 11
Thus the first meeting at 12 hour mark will take place exactly after (12/11 + 12/13 + 2)*65 + 12/11 = 262 hours. That is a lot sooner than 573 hours calculated in step 1.
All that is relatively easy to figure out using regular fractions and modular arithmetic. But it does not hurt to verify using the angles in degrees in decimals as calculated by TSLF.
The first step of the cycle the hour hand travels (12/11)*360/12 = 32.72(72).... degrees.
On the third cycle step, the hour hand travels (12/13)*360/12 = 27.69231... degrees.
Making the full cycle: 32.7272(72) + 27.692308 = 60.41958...
After 65 full cycles plus the first step of the next cycle the hour hand travels 60.41958.. * 65 + 32.7272(72) = 3960 (exactly). Which also happens to be divisible by 360. 3960 / 360 = 11.
And so all 12-hour mark meetings' elapsed times are as following:
262 + 574*n
263 + 574*n
573 + 574*n
574 + 574*n
The first meeting is after 262 hours.
-
 1
1
-
-
1). Specifying numeric values for angles and sides is not enough. You can build up to 6 different convex quadrilaterals given four sides and one angle. Up to 3 different triangles given two sides and one angle.
To construct a polygon from given sides and angles, must know where they are in relation to one another.
2). Given n-1 angles for n-gon, we can figure out the n-th angle on our own. It does not represent any additional piece of information.
Or to put it differently, cannot leave more than 2 sides unspecified.
3). It would not hurt to ask whether the shape is not concaved. If it is -- must find out all the angles or the pairs of sides that are concaved before embarking on the figure building project.Given the above, the formula is 2n - 3, as has been already noted.
That would be minimum and sufficient information to build an n-gon. I.e.:
Shape.......Minimum and sufficient
triangle ...........3
quadrilateral ...5
pentagon.........7
etc.-
 1
1
-
-
For the tangential straight line escape the problem has been solved. The method of escape dictated construction of the equations finding the values for
r and Ogre/Maiden speed ratio. That path also determines the angle the Ogre has to travel. For the landing points past the tangential and bigger angular travels by Ogre, consider the following.
The shortest path to such point is around the small circle perimeter and then on a straight tangential line. Any other curved or segmented path is longer and must be rejected by clever maiden. But then all it comes down to is the same tangential escape only delayed.This puzzle bears some logical inferences, which allow to dispense with extra complex math. Just what we all like in puzzles.
-
You need at least one side length among your three pieces of information for a triangle. Three angles won't do.
-
Define:
- azimuth - the angle with regard to the center of the lake.
Zero at ogre's starting position and increasing in a clockwise direction.
- gap - the angle from ogre to maiden, measured in the ogre's direction of pursuit.
- w - the ogre's azimuthal speed = s/R where s = 4R/hour where R = lake radius.
Thus w = 4 radians/hour.
- r - the radius of safety that depends on maiden's top speed:
an inner circle inside which maiden can achieve w, and outside of which she cannot.
Pre-chase maneuvering:
Within the circle of safety, maiden achieves the optimal starting position for the chase:
- Ogre's azimuth is 0
- Maiden's azimuth is 180 on the safety circle perimeter
- Gap = 180 [maximum]
- Distance from ogre: R+r [maximum]
- Distance to shore: R-r [minimum]
Objectives:
- Maiden: Survival = reach shore before the gap becomes 0.
- Ogre: Capture = reduce gap to 0 before maiden reaches shore.
- Us: Find the lowest maiden speed for which she can achieve simultaneous arrival on shore.
This means find the best escape path to permit escape at the lowest maiden speed.
Progess so far:
Maiden speed = Ogre speed / 4.6033 gets maiden to shore on tangential path, arriving simultaneously with ogre.
Now let's try to improve on 4.6033.
Here are my conjectures: comments are welcome
- When the chase begins, Maiden leaves, and then never re-enters the circle of safety.
[a] if she re-enters, she can only re-set the race at the optimal starting position
. - Ogre will maintain the maximum speed of w, meaning that at any moment his only strategy is to choose CW or CCW pursuit.
[a] If he were to stop, maiden improves her position by heading directly away from him,
eventually landing on the opposite shore with gap = 180.
If he were to slow down, maiden's relative speed increases, and she moves more efficiently toward shore.
[a] maiden cannot match ogre's angular speed of w unless she re-enters the circle of safety. She won't. See above.
if gap were to increase, it means ogre is moving in the wrong direction, which he instantaneously reverses.
Ogre will never zig zag, meaning that ogre's only strategy is initial choice of direction. Nothing else. Then run full speed.[a] At the outset of the chase, an infinitessimal motion by maiden dictates ogre's initial choice of direction [CW or CCW].
At any point thereafter, if ogre changes direction he will increase the gap.
[c] At any point thereafter, if maiden changes direction she will decrease the gap.
[d] Therefore, neither will ever change their angular direction.
Maiden's best initial direction is tangential[a] That direction initially matches ogre's angular speed of w.
It begins her radial journey toward R keeping the decrease of gap at a minimum.
[c] Thereafter, it remains to be found the best way to add a radial component to her escape path.
The next step is to answer these questions:
- Will spiraling away from ogre get her to shore with a greater gap than for a straight line?
- If so, what is the optimal curvature of that spiral?
Approach for determining the advantage if any for a spiral path:
Straight-path analysis was simple enough to permit solving directly for maiden speed that gave simultaneous arrival. For spiral path analysis to be equally tractable, its curvature [non zero] will have to be specified.
Analysis for spiral.
Write rm = r + m.THETA where THETA increases CW from maiden's initial position.
Landing point will be the THETA for which rm = R.
The PATH LENGTH of the spiral can be calculated.
THETA and PATH LENGTH are substituted into the equations used in the straight-line analysis to determine the speed ratio f.
So we do this several times, for different values of m.
One value of m will give a smallest maiden speed - i.e. highest value of f.
That will be the optimum spiral escape path.
The problem I'm having at present is integrating the spiral equation to obtain path length.
Disturbing result!
I ran the straight line analysis to send the boat to the 3 pi / 2 landing point.
That is just slightly farther down the shore for ogre.
The speed ratio decreased from the tangential value of 4.6033 to 4.500...
I did not expect that.
Perhaps tangential straight line escape is optimal.
It seems, you have proven that the tangential straight line escape is the optimal path. I'll try to put put a simpler perspective on this whole Ogre-Maiden business using BMAD's “Dog Freedom” recent problem in this forum.
The “gap” and Ogre's angular speed simplify things quite a bit.
Imagine a solid wall rising around the Maiden's inner circle r when she leaves its perimeter at the escape point E. A thin rigid rod pivoted at the center of the lake extends from Ogre across the entire lake. As Ogre runs, he rotates the rod painting the angle α. (Somehow, the wall does not interfere with the rod.)
The distance traveled by the maiden is α*r along the perimeter of her inner circle, or any other path outside it. The intersection point between the rod and tangential path is at r*tan α dangerously close to the distance α*r traveled by the maiden. Looks like if she just swerved to the right she could catch that rod and get herself a new better head start. But then our work would be invalidated.
Say, some optimal curve existed leading to the landing point L1, but then we could draw a straight line to the same point as shown on the diagram, thus invalidating that curve as optimal. Straight line is shorter, and as long as it does not catch the moving rod, a better valid path.
Suppose we found what we are looking for – the overall angle α traveled by Ogre and the optimal r. Then we could make a leash of the length α*r, tie one end to the point E, the other – to the boat. Pulling at the maiden's end of the leash, intersect it with the shore. If the end of the leash extends past the shore, rotate to the right while keeping the tension until the boat rests exactly at the edge of water, and, so happens, at the optimal α.
No curve constructed of the same leash can beat that. If the leash wraps a bit around the wall instead of just touching it at E, then it's too long. It simply resets the points E and O.
The lower boundary for the length of the leash is α*r >= R – r (otherwise it cannot reach the shore.)
In the post #34 I gave the formula for the straight line escape routes between nearest point escape L0 and tangential escape Lt. That function has its minimum value at the boundary point Lt.
It appears, there is no spiral escape. But don't tell the maiden.
- azimuth - the angle with regard to the center of the lake.
-
22. The difficult cases are the ones where all the weights are the same, or where only one of them is different. A reference weight of 22 allows one to discriminate these cases well. For example, suppose all of the weights are 6 grams except for one which is less. You can determine that all of the others are 6 by observing that 4 of them weigh more than the reference weight, and that they all weigh the same as one another. To determine the weight of the "extra" one, add it to three of the other stones and compare against the reference weight. If it is greater, the extra stone weighs 5 grams; if equal, it weighs 4; if less, combine it with the reference weight and compare against four of the other stones. If it is greater, it is 3 grams; if equal, it is 2 grams; if less, it is 1 gram. Similar reasoning seems to work with stones that are each 5 grams...
I suspect, your suspicion is correct. That's the same reference weight that I found. There is a certain criteria for it.
Rather than enumerating all different cases, I invite all participants to try and find cases, which would be indistinguishable with this reference weight.
K-man came close to the solution and was the first to "think outside the box",
Noting that the reference weight does not need to be within the range of stone weights.
Larger weights solve the single lighter stone among 11 6g stones, but they don't work for one heavy stone among 11 1g stones. With 22g reference weight how will you identify the weight of a single heavy stone among 11 1g stones?
When you have 11 equal stones, which put together are lighter than 22 g., you know those are 1 g. stones. Now you can use them as reference weights to measure whatever remaining heavier stone you have.
In a way, this problem is a mix of weighing problem and sort.
-
22. The difficult cases are the ones where all the weights are the same, or where only one of them is different. A reference weight of 22 allows one to discriminate these cases well. For example, suppose all of the weights are 6 grams except for one which is less. You can determine that all of the others are 6 by observing that 4 of them weigh more than the reference weight, and that they all weigh the same as one another. To determine the weight of the "extra" one, add it to three of the other stones and compare against the reference weight. If it is greater, the extra stone weighs 5 grams; if equal, it weighs 4; if less, combine it with the reference weight and compare against four of the other stones. If it is greater, it is 3 grams; if equal, it is 2 grams; if less, it is 1 gram. Similar reasoning seems to work with stones that are each 5 grams...
I suspect, your suspicion is correct. That's the same reference weight that I found. There is a certain criteria for it.
Rather than enumerating all different cases, I invite all participants to try and find cases, which would be indistinguishable with this reference weight.
K-man came close to the solution and was the first to "think outside the box",
Noting that the reference weight does not need to be within the range of stone weights.
-
Part 2: you can have as many stones as you want. Which stones? Reference stones of my two chosen denominations? Or as many unknown stones?
For the part 2, you can have 2 reference weights of your choice, as many stones as you want in the weight range from 1 to N. (Must find the largest N and the 2 reference weights.)
Let's solve the first part first. No tricks, no cheating, no different interpretations of the OP. If there is an ambiguity, I'll clarify it.


Give a monkey enough rope
in New Logic/Math Puzzles
Posted
Nice. Whereas one of the two Google founders was born in Moscow.
You must know Russian to appreciate and fully enjoy the beauty of the translation.
The first sentence of the translation actually is: The rope [to] pulley had ran up to ... (As if the rope or pulley had legs and actually ran. Hard to say which.)
Working off the OP in English with some aid of Russian translation I get a very large negative weight for the rope.