[Who gets a free dinner?]

I'd like to enter the following solution and claim the minimum number of throws.

Divide the entire table cloth into n rectangles of equal area with a permanent marker. Each participant must be assigned his rectangle. Then ask the waiter to throw the coin onto the table cloth from afar.

[Who gets a free dinner?]

I want to be a party pooper.

Thought about it some more I I think I have an algorithm that would do it more efficiantly

Suppose at some stage in this proccess we have k people.

If k is even, split the group in 2, asign each a side of the coin and flip it, discard the incorrect group (how you split into 2 and choose who is heads is irrelivent since the coin toss randomises it whatever the case).

If k is odd remove someone from the group and do the same as above to the remaining even-numbered group, for the additional person flip the coin to determain where they are discarded or not. This is fair on everyone as each individual has a 50/50 chance of being discarded.

Eventually there will only be 1 person remaining.

This one is unfair.

Example

Consider decision between 3 participants. For either of the two guys who were paired against each other in the first round the probability of win is winning the first round and the 3rd man not advancing to finals, plus winning the first round and the finals, should the 3rd man advance. Or 1/4 + 1/8 = 3/8.
The man who plays the first round by himself, must always win two rounds, his probability is 1/4.

Flip the coin 1+floor(log(base2)(n)) times, record a 1 for each heads and a 0 for each tails to get a binary number, also assign each person a number between 1 and n. The person you choose is the one with the number which is equal to the binary number once it has been converted into decimal.

Nice. However, as Bushindo has noticed this one may require replay for number of participants other than power of 2. So there is no ceiling on how many coin throws decide the winner.

You're out with friends at Chuck's Steak House and decide to flip a coin to select one person get a free dinner. The bill will be split n-1 ways instead of n ways. Since I was not invited, I don't know how many are in the group. (Maybe next time you'll include me; I love Chuck's place.) So anyway, your selection method has to work for an arbitrary numbers of participants.

You have only a fair coin, and the method has to treat everyone equally.
It must be absolutely fair and unbiased.

There might be many ways; bonus points await methods with originality, flair, and minimization of flips.

Pick one person out of n, fairly, with a sequence of fair coin tosses.

I'm trying to go for the minimum expected number of flips here. This is my best attempt so far

If N is a power of 2, the solution is trivial. Let's assume N is not a power of 2. Divide the interval from 0 to 1 into N sub-intervals. Each person will be assigned a sub-interval. So, if there are 3 participant, the first one would be assigned [0, 1/3), the second [1/3, 2/3), and the third [2/3, 1].

Flip the coin and treat the resulting string of outcomes as a fractional binary number. For instance, let head = 1 and tail = 0. If we flip head two times in a row, that is the equivalent of .11 in binary or (1/2 + 1/4 = .75 in decimal). Let the fractional binary number we construct after N flip be B_N. The range of values for the binary number B_infinity after the first N flip is [b_N,B_N + 2^-N].

So, let's say after two flips the binary number is .11 in binary or .75 in decimal. The range of possible binary number, assuming an infinite number of continuing flips, in decimal form is [.75, 1].

The idea is as soon as the possible values [b_N,B_N + 2^-(N) ] is entirely contained within 1 person's subinterval, that person is selected.

Let's calculate the expected number of flips required. For N participants where N is not a power of 2, we would require ceiling( log2( N ) ) flips to narrow the field down to two people. From there it takes an expected number of 2 further flips to further select one of those two. That gives us an upper bound of ceiling( log2( N ) ) + 2 for the expected number of flips.

Awesome. Same problem though – no ceiling. And it seems fair, but not in an obvious way. A proof of fairness would be nice.

[Four darts]

My first thought when I read this was about areas. Given a triangle on a unit circle the probablility of a 4th point (dart) being in the triangle is (the area of the triangle)/Pi. The average area of a triangle in a unit circle is 35/(48Pi). So wouldn't that make the probablility of the 4th dart being in the triangle 35/(48Pi²) or approx. .07388? This is how I see this problem working in my mind.

If we know the average area of a randomly drawn triangle inside a unit circle, then the problem is solved. How do you find the average area of triangle? Where does 35/48Pi come from?

http://mathworld.wolfram.com/DiskTrianglePicking.html

But that's not solving the puzzle, that's finding an answer on the internet. I don't understand 5-tuple integrals and would have to study to verify that solution.

It is educational. However, to discover something of our own, I'd look for a simpler more understandable solution.

[Four darts]

The history of this problem as I recall it.

I suggested first solving the average distance between two points inside the unit circle. Then solving the average distance from a point to a segment inside the unit circle. Thus finding the average area of triangle and ultimately solving the problem.

I don't recall that anyone coming up with a solid analytical solution. Bonanova ran computer simulations providing the numeric answer and came up with analysis, which I did not quite follow at the time.

There was some confusion about the 4th point inside the triangle formed by the first 3 points, versus concave quadrilateral. I belive I resolved that question this time around in the post #3 with corrections by Bushindo in post #4.

[Four darts]

My first thought when I read this was about areas. Given a triangle on a unit circle the probablility of a 4th point (dart) being in the triangle is (the area of the triangle)/Pi. The average area of a triangle in a unit circle is 35/(48Pi). So wouldn't that make the probablility of the 4th dart being in the triangle 35/(48Pi²) or approx. .07388? This is how I see this problem working in my mind.

If we know the average area of a randomly drawn triangle inside a unit circle, then the problem is solved. How do you find the average area of triangle? Where does 35/48Pi come from?

[Four darts]

Since question 1 was not a part of that problem posted in 2008, let me provide a solution to that one real quick.

Let's say the probability of 4 darts forming a convex quadrilateral is

P.

Then probability of the 4th dart hitting inside the triangle formed by the first three is P/4.

Proof:

Any convex quadrilateral forms a triangle with the 4th point inside, and from any triangle with a point inside 3 different quadrilaterals may be formed.

Any 4 points may be ordered in 4! = 24 ways. Whereas any 3 points may be ordered in 3! = 6 ways. 3!/4! = 1/4.

Now, that question 1 is solved, I am inclined to yield the opportunity of solving question 2 to others.

I think the proof is fine as it is, but I believe there are a few typos. See below

Quoting Prime:

****************

Let's say the probability of 4 darts not forming a convex quadrilateral is P (i.e., P = probability the four darts form a triangle enclosing 1 point).

Then probability of the 4th dart hitting inside the triangle formed by the first three is P/4.

Proof:

Any convex quadrilateral forms a triangle with the 4th point inside outside, and from any triangle with a point inside outside 3 different quadrilaterals may be formed.

Any 4 points may be ordered in 4! = 24 ways. Whereas any 3 points may be ordered in 3! = 6 ways. 3!/4! = 1/4.

Question for bonanova: about question 1- the probability that the 4th point falls within the triangle,

So the problem is equivalent to finding the area of a triangle given 3 points, and then integrating that area over the distribution of those 3 points.

We need 2 coordinates to describe a single point in the circle, so we would need 6 coordinates (x₁, y₁, x₂, y₂, x₃, y₃) to describe any distribution of 3 points.

There is a straight forward formula for computing the area of a triangle given 3 points. As such, we can construct a sextuple integral for compute the solution. (Solving the integral analytically might be a problem, though the integral might be evaluated by numerical means)

I assume that such a sextuple integral is not acceptable as a solution =)?

Yes, I muddled my explanation. Of course, I meant not forming convex quad, or forming concave quad. But I did mean the point inside a triangle. Perhaps, I should have mentioned re-drawing the lines connecting the points.

At any rate, my post solves the relation between question 1 and question 2.

The straightforward approach with sixtuple integral seems too complex and more a numeric than analytical solution. As far as I remember, Bonanova had done numeric solution back when, by runnig computer simulations.

[Four darts]

Since question 1 was not a part of that problem posted in 2008, let me provide a solution to that one real quick.

Let's say the probability of 4 darts forming a convex quadrilateral is

P.
Then probability of the 4th dart hitting inside the triangle formed by the first three is P/4.

Proof:
Any convex quadrilateral forms a triangle with the 4th point inside, and from any triangle with a point inside 3 different quadrilaterals may be formed.
Any 4 points may be ordered in 4! = 24 ways. Whereas any 3 points may be ordered in 3! = 6 ways. 3!/4! = 1/4.

Now, that question 1 is solved, I am inclined to yield the opportunity of solving question 2 to others.

[Four darts]

I recall vaguely, trying to solve that problem. I seem to recall we did not come to a consensus back then. It seems like a serious math problem. And we were trying to solve only the question 2 there.

[For Bushindo - (others try at your own risk)]

Now Bushindo is with Bonanova insisting that Win(shooting air)=Win(shooting Alex) means uncertainty. What's wrong with my tiebreaks?

A true 3-way duel indeed. But all got the same answer to the problem.

I can see where my guidlines to Cole in post#4 could be misinterpreted. My intention was to help Cole avoiding computations, where possible. For if he sits down with a calculator in the middle of the duel, the other two guys may get angry and just shoot him out of turn.

I think I misinterpreted your position. I don't think bononova and I share the same interpretation of 'uncertain', though. Let me see if we have the following positions correct

bonanova: 'Uncertain' means being unable to tell whether W_{shoot_air}(b,c) < W_{shoot_at_Alex}(b,c) or W_{shoot_air}(b,c) > W_{shoot_at_Alex}(b,c) without applying those functions. So, Cole is uncertain between .31 < b < .39.

bushindo: 'Uncertain' means W_{shoot_air}(b,c) = W_{shoot_at_Alex}(b,c).

Prime: 'Uncertain' means being unable to make a decision based on all available information. There is no situation when Cole is uncertain about what to do next. Cole should always choose the strategy that gives higher value between W_{shoot_air}(b,c) and W_{shoot_at_Alex}(b,c).

I agree that under the standard dictionary definition of 'uncertain', Prime's interpretation would be most correct. I thought that bonanova had some different specialized meaning in mind, and apparently he does. It just isn't what I thought it was =).

The way I see it, Bonanova has made his problem statement/position 100% clear:

Uncertainty is when Cole's winning chance by shooting in the air = his winning chance by shooting at Alex.

The question Bonanova wants us to solve is: For what values of b (accuracy of Bobby) such situation is possible?

And solved it we have:

And we all (including Bonanova) have found same equation yielding the same answer:

When b is between 31.8% and 38.2% that "uncertainty" may occur.

For the values of b outside those boundaries, a situation where W_{shoot_air}(b,c) = W_{shoot_at_Alex}(b,c) is impossible.

Bushindo's view of uncertainty is the same as Bonanova's: W_{shoot_air}(b,c) = W_{shoot_at_Alex}(b,c).

However, there seems to be some uncertainty as to what exactly Bonanova wants us to find.

Prime picks on the usage of the word uncertain. Does not believe there is any uncertainty here at all. (When chances are equal, Cole must shoot Alex, because he hates him more than he hates Bobby.) Also, Prime promotes (unsuccessfully) an alternative strategy whereby Cole shoots himself in the foot with his very first shot.

[For Bushindo - (others try at your own risk)]

Let me try and bring consensus here by wearing everyone down with a lengthy, unnecessarily tedious, and tiresome detailed solution.

Outside of solving inequality, which I think is more revealing than equality, I don't see any significant difference in the results. I did use a little shortcut without giving an adequate explanation/justification for it. Therefore, I feel compelled to clarify the point where the reasoning ends and algebra begins.

I'll stick to my nomenclature: probability of Bobby hitting target = b; probability of Cole hitting target = c. (To avoid typing subscripts.)

If Cole shoots in the air, then Bobby shoots at Alex.

1) If Bobby misses, Alex kills Bobby and Cole gets just one shot at Alex.

2) If Bobby kills Alex then it is a duel between Cole and Bobby, with Cole shooting first. Cole's chance in that duel (D) is:

D = c + (1-c)(1-b)D; From which we find: D = c/(1 - (1-b)(1-c)) = c/(b+c-bc).

Thus Cole's survival probability if he shoots in the air (A) is:

A = (1-b)c + bD = (1-b)c + bc/(b+c-bc).

Now, here is the justification for the shortcut I used. If it suits my purposes, I can substitute A as following:

A = (1-c)A + cA. (It is perfectly legitimate algebraic substitution.)

If Cole shoots at Alex, then:

1) Cole hits the air instead at the probability of (1-c). Thereafter, it is the same scenario as when Cole hit the air on purpose. With overall Cole's survival probability in this variation:

(1-c)A.

2) Cole hits Alex at the probability of c. Then Bobby gets the first shot at Cole. We are not interested in variation where Bobby hits Cole, since we are calculating Cole's survival chances. So if on his first shot Bobby misses Cole at the probability of (1-b), then it is the same duel with Cole's first shot. Thus the probability of Cole's survival in this situation is

c(1-b)D = c²(1-b)/(b+c-bc).

Overall, Cole's probability of survival when shooting at Alex (S) is:

S = (1-c)A + c(1-b)D = (1-c)((1-b)c + bc/(b+c-bc)) + c²(1-b)/(b+c-bc).

Now we must compare the two strategies. And find that when A > S, we shall advise Cole to shoot in the air.

A > S;

(1-c)A + cA > (1-c)A + c(1-b)D.

Here we notice that we can eliminate the term (1-c)A from both sides of equation. That was the shortcut I used.

cA > c(1-b)D.

A > (1-b)D, (since c is positive, not equal zero.)

Now I drop all reasoning and just use algebra:

(1-b)c + bc/(b+c-bc) > (1-b)c/(b+c-bc)

(1-b) + b/(b+c-bc) > (1-b)/(b+c-bc), again, since c is positive not equal zero.

1-b > (1-2b)/(b+c-bc). Note, that for b and c between zero and 1, b+c-bc > 0, therefore:

(1-b)(b+c-bc) > 1-2b

c-2cb+cb²> 1-3b+b²

c(1-2b+b²) > 1-3b+b²

c > (1-3b+b²)/(1-b)² (given that (1-b)² > 0). (Same as Bushindo, except for the b² instead of b³ in the numerator.)

c > ((1-b)² - b))/(1-b)²

c > 1 - b/(1-b)²

Let's study 1 - b/(1-b)², or (1-3b+b²)/(1-b)².

We know that 0 < b < 1. As b increases the function decreases. Solving for zero, and omitting the greater than 1 root, we get:

b = (3-sqrt(5))/2.

That is the value of b above which the expression yields negative numbers. And since we know that c is positive, we can draw the conclusion that for the values of b above that boundary, Cole is always at advantage when making his first shot in the air. Approximating that as a percentage yields 38.1966%. When Bobby is a is a better shot than 38.2%, Cole must shoot in the air without giving it a second thought.

Another boundary condition is where the expression yields values greater than b. Since we know that c < b, past the boundary of b = (1-3b+b²)/(1-b)², the values of c satisfying the inequality contradict the condition that Bobby is a better shot than Cole. Solving cubic equation, we find that the approximate value b=0.317672 or 31.7672% is that boundary. If Bobby shoots worse than 31.7672%, Cole must try and shoot Alex.

If Bobby shoots in between those boundary conditions (31.7672% < b < 38.1966%), Cole must evaluate the expression 1 - b/(1-b)² and compare his shooting prowess c to the result. If c is better, Cole must shoot in the air, if c is less – aim at Alex. If c happens to be exactly equal, for example b=35% and c=17.1598%, then Cole must decide who he hates more: Alex or Bobby. If Cole shoots in the air first, Alex's survival is (1-b)(1-c), if Cole aims at Alex, Alex's survival chance becomes (1-c)(1-b)(1-c). If Cole hates Alex and Bobby exactly equally, then he must shoot in the air – a noble gesture.

At no time there is any uncertainty, save for the wacky cases c=0, or b=1.

Hopefully, this solves all tiebreak situations and removes the uncertainty.

Reading from the OP:

Given that it [Cole's strategy] is uncertain, what can we determine regarding Bobby's shooting accuracy?

From your reasoning regarding Cole's strategy, what is the answer?

I agree about semantics. I think the underlying crux of the discussion is the interpretation of 'uncertain'

From above, it is easy to derive the expression for the chance of Cole winning if he shoots into the air and if he shoots at Alex. Let's denote those functions W_{shoot_air}(b,c) and W_{shoot_at_Alex}(b,c), respectively.

Prime and bonanova seems to interpret 'uncertain' as being unable to tell whether W_{shoot_air}(b,c) < W_{shoot_at_Alex}(b,c) or W_{shoot_air}(b,c) > W_{shoot_at_Alex}(b,c) without applying those functions. Indeed, between .31 < b < .39, Cole must be able to apply those function in order to see which strategy gives a higher winning probability.

My interpretation is that, since W_{shoot_at_Alex}(b,c) and W_{shoot_air}(b,c) are easily derivable and b and c are known, Cole is 'uncertain' if the two strategies give precisely the same survival probability. That is, W_{shoot_air}(b,c) = W_{shoot_at_Alex}(b,c).

I have no objection to the interpretation of Prime and bonanova, except that it should be qualified to prevent confusion. In post #4, Prime did indicate that between .31 < b < .39, Cole should compute W_{shoot_air}(b,c) and W_{shoot_at_Alex}(b,c) to determine the better strategy. Presenting the result without the qualification as in post #8 may mislead the reader into thinking that the two strategies are the same within .31 < b < .39.

Now Bushindo is with Bonanova insisting that Win(shooting air)=Win(shooting Alex) means uncertainty. What's wrong with my tiebreaks?

A true 3-way duel indeed. But all got the same answer to the problem.

I can see where my guidlines to Cole in post#4 could be misinterpreted. My intention was to help Cole avoiding computations, where possible. For if he sits down with a calculator in the middle of the duel, the other two guys may get angry and just shoot him out of turn.

[Give a monkey enough rope]

Somehow, I see paragraph 2 differently.

I see paragraph 2 this way:

weight = rope + 2*(2*3*3a - 1.125a) -2.25a

When the narrative says "was when," or "will be when,"

denote that time frame by an offset of a, b, c, d ... years.

So "... monkey was years old when (x-a) mother was (y-a)

twice as old as brother was when (z-b) mother was (y-b)

half as old as brother will be when (z-c) brother is (z-c)

three times as old as mother was when (y-d) mother was (y-d)

three times as old as monkey was (x) in paragraph 1.

This says

y-a = 2(z-b)

y-b = (z-c)/2

z-c = 3(y-d)

y-d = 3x

The whole paragraph says W = L/4 + (x-a).

Eliminate a, b, c, d, and use z = (x+y)/2.

That's not what paragraph 2 says in the OP.

You're right. OP is corrected.

I was presumptuous to teach you how to solve ...

Apologies.

Thanks. That brings it closer. I get a positive weight rope now, alas, not enough for the monkey and the rope together to balance the weight.

The way I see paragraph 2 now:

Weight - rope = ((3*3a)/2 -1.125a)*2 - 2.25a = 4.5a. (Where a=16/17).

Whereas, Weight + rope = 4.875a (from paragraph 1). Leaving the weights as 0.1875a for the rope weight, 4.6875a for the weight, and 3.25a for the monkey. Where the monkey together with the entire rope cannot outweigh the weight.

[For Bushindo - (others try at your own risk)]

Let me try and bring consensus here by wearing everyone down with a lengthy, unnecessarily tedious, and tiresome detailed solution.

Outside of solving inequality, which I think is more revealing than equality, I don't see any significant difference in the results. I did use a little shortcut without giving an adequate explanation/justification for it. Therefore, I feel compelled to clarify the point where the reasoning ends and algebra begins.

I'll stick to my nomenclature: probability of Bobby hitting target = b; probability of Cole hitting target = c. (To avoid typing subscripts.)

If Cole shoots in the air, then Bobby shoots at Alex.

1) If Bobby misses, Alex kills Bobby and Cole gets just one shot at Alex.

2) If Bobby kills Alex then it is a duel between Cole and Bobby, with Cole shooting first. Cole's chance in that duel (D) is:

D = c + (1-c)(1-b)D; From which we find: D = c/(1 - (1-b)(1-c)) = c/(b+c-bc).

Thus Cole's survival probability if he shoots in the air (A) is:

A = (1-b)c + bD = (1-b)c + bc/(b+c-bc).

Now, here is the justification for the shortcut I used. If it suits my purposes, I can substitute A as following:

A = (1-c)A + cA. (It is perfectly legitimate algebraic substitution.)

If Cole shoots at Alex, then:

1) Cole hits the air instead at the probability of (1-c). Thereafter, it is the same scenario as when Cole hit the air on purpose. With overall Cole's survival probability in this variation:

(1-c)A.

2) Cole hits Alex at the probability of c. Then Bobby gets the first shot at Cole. We are not interested in variation where Bobby hits Cole, since we are calculating Cole's survival chances. So if on his first shot Bobby misses Cole at the probability of (1-b), then it is the same duel with Cole's first shot. Thus the probability of Cole's survival in this situation is

c(1-b)D = c²(1-b)/(b+c-bc).

Overall, Cole's probability of survival when shooting at Alex (S) is:

S = (1-c)A + c(1-b)D = (1-c)((1-b)c + bc/(b+c-bc)) + c²(1-b)/(b+c-bc).

Now we must compare the two strategies. And find that when A > S, we shall advise Cole to shoot in the air.

A > S;

(1-c)A + cA > (1-c)A + c(1-b)D.

Here we notice that we can eliminate the term (1-c)A from both sides of equation. That was the shortcut I used.

cA > c(1-b)D.

A > (1-b)D, (since c is positive, not equal zero.)

Now I drop all reasoning and just use algebra:

(1-b)c + bc/(b+c-bc) > (1-b)c/(b+c-bc)

(1-b) + b/(b+c-bc) > (1-b)/(b+c-bc), again, since c is positive not equal zero.

1-b > (1-2b)/(b+c-bc). Note, that for b and c between zero and 1, b+c-bc > 0, therefore:

(1-b)(b+c-bc) > 1-2b

c-2cb+cb²> 1-3b+b²

c(1-2b+b²) > 1-3b+b²

c > (1-3b+b²)/(1-b)² (given that (1-b)² > 0). (Same as Bushindo, except for the b² instead of b³ in the numerator.)

c > ((1-b)² - b))/(1-b)²

c > 1 - b/(1-b)²

Let's study 1 - b/(1-b)², or (1-3b+b²)/(1-b)².

We know that 0 < b < 1. As b increases the function decreases. Solving for zero, and omitting the greater than 1 root, we get:

b = (3-sqrt(5))/2.

That is the value of b above which the expression yields negative numbers. And since we know that c is positive, we can draw the conclusion that for the values of b above that boundary, Cole is always at advantage when making his first shot in the air. Approximating that as a percentage yields 38.1966%. When Bobby is a is a better shot than 38.2%, Cole must shoot in the air without giving it a second thought.

Another boundary condition is where the expression yields values greater than b. Since we know that c < b, past the boundary of b = (1-3b+b²)/(1-b)², the values of c satisfying the inequality contradict the condition that Bobby is a better shot than Cole. Solving cubic equation, we find that the approximate value b=0.317672 or 31.7672% is that boundary. If Bobby shoots worse than 31.7672%, Cole must try and shoot Alex.

If Bobby shoots in between those boundary conditions (31.7672% < b < 38.1966%), Cole must evaluate the expression 1 - b/(1-b)² and compare his shooting prowess c to the result. If c is better, Cole must shoot in the air, if c is less – aim at Alex. If c happens to be exactly equal, for example b=35% and c=17.1598%, then Cole must decide who he hates more: Alex or Bobby. If Cole shoots in the air first, Alex's survival is (1-b)(1-c), if Cole aims at Alex, Alex's survival chance becomes (1-c)(1-b)(1-c). If Cole hates Alex and Bobby exactly equally, then he must shoot in the air – a noble gesture.

At no time there is any uncertainty, save for the wacky cases c=0, or b=1.

Hopefully, this solves all tiebreak situations and removes the uncertainty.

Reading from the OP:

Given that it [Cole's strategy] is uncertain, what can we determine regarding Bobby's shooting accuracy?

From your reasoning regarding Cole's strategy, what is the answer?

We are arguing semantics. To me uncertain means cannot be determined, like division by zero. I just do not see the choice between two equally good (bad) values as an uncertainty. And I have given several good ways to decide the tiebreak. I don't think it's all that important in our three way duel. I figure, Bushindo's objection was to omitting inclusion of all of the variations into the equation. I think we are in the right to do that. And after algebraic simplifications the full equations would come to the same thing. And we all use different nomenclature. (Mine is the easiest to type, although not as formal.)

I found it interesting that in Bonanova's analysis, using probability of missing (q), simplifies the solution. In particular the solution of the cubic equation.

I say, this duel is solved.

Alternatively, shooting himself in the foot may be the best option for Cole.

[For Bushindo - (others try at your own risk)]

Let me try and bring consensus here by wearing everyone down with a lengthy, unnecessarily tedious, and tiresome detailed solution.

Outside of solving inequality, which I think is more revealing than equality, I don't see any significant difference in the results. I did use a little shortcut without giving an adequate explanation/justification for it. Therefore, I feel compelled to clarify the point where the reasoning ends and algebra begins.

I'll stick to my nomenclature: probability of Bobby hitting target = b; probability of Cole hitting target = c. (To avoid typing subscripts.)

If Cole shoots in the air, then Bobby shoots at Alex.
1) If Bobby misses, Alex kills Bobby and Cole gets just one shot at Alex.
2) If Bobby kills Alex then it is a duel between Cole and Bobby, with Cole shooting first. Cole's chance in that duel (D) is:
D = c + (1-c)(1-b)D; From which we find: D = c/(1 - (1-b)(1-c)) = c/(b+c-bc).

Thus Cole's survival probability if he shoots in the air (A) is:
A = (1-b)c + bD = (1-b)c + bc/(b+c-bc).
Now, here is the justification for the shortcut I used. If it suits my purposes, I can substitute A as following:
A = (1-c)A + cA. (It is perfectly legitimate algebraic substitution.)

If Cole shoots at Alex, then:
1) Cole hits the air instead at the probability of (1-c). Thereafter, it is the same scenario as when Cole hit the air on purpose. With overall Cole's survival probability in this variation:

(1-c)A.
2) Cole hits Alex at the probability of c. Then Bobby gets the first shot at Cole. We are not interested in variation where Bobby hits Cole, since we are calculating Cole's survival chances. So if on his first shot Bobby misses Cole at the probability of (1-b), then it is the same duel with Cole's first shot. Thus the probability of Cole's survival in this situation is

c(1-b)D = c²(1-b)/(b+c-bc).

Overall, Cole's probability of survival when shooting at Alex (S) is:
S = (1-c)A + c(1-b)D = (1-c)((1-b)c + bc/(b+c-bc)) + c²(1-b)/(b+c-bc).

Now we must compare the two strategies. And find that when A > S, we shall advise Cole to shoot in the air.

A > S;
(1-c)A + cA > (1-c)A + c(1-b)D.
Here we notice that we can eliminate the term (1-c)A from both sides of equation. That was the shortcut I used.
cA > c(1-b)D.
A > (1-b)D, (since c is positive, not equal zero.)

Now I drop all reasoning and just use algebra:
(1-b)c + bc/(b+c-bc) > (1-b)c/(b+c-bc)
(1-b) + b/(b+c-bc) > (1-b)/(b+c-bc), again, since c is positive not equal zero.
1-b > (1-2b)/(b+c-bc). Note, that for b and c between zero and 1, b+c-bc > 0, therefore:
(1-b)(b+c-bc) > 1-2b
c-2cb+cb²> 1-3b+b²
c(1-2b+b²) > 1-3b+b²
c > (1-3b+b²)/(1-b)² (given that (1-b)² > 0). (Same as Bushindo, except for the b² instead of b³ in the numerator.)
c > ((1-b)² - b))/(1-b)²
c > 1 - b/(1-b)²

Let's study 1 - b/(1-b)², or (1-3b+b²)/(1-b)².
We know that 0 < b < 1. As b increases the function decreases. Solving for zero, and omitting the greater than 1 root, we get:
b = (3-sqrt(5))/2.
That is the value of b above which the expression yields negative numbers. And since we know that c is positive, we can draw the conclusion that for the values of b above that boundary, Cole is always at advantage when making his first shot in the air. Approximating that as a percentage yields 38.1966%. When Bobby is a is a better shot than 38.2%, Cole must shoot in the air without giving it a second thought.

Another boundary condition is where the expression yields values greater than b. Since we know that c < b, past the boundary of b = (1-3b+b²)/(1-b)², the values of c satisfying the inequality contradict the condition that Bobby is a better shot than Cole. Solving cubic equation, we find that the approximate value b=0.317672 or 31.7672% is that boundary. If Bobby shoots worse than 31.7672%, Cole must try and shoot Alex.

If Bobby shoots in between those boundary conditions (31.7672% < b < 38.1966%), Cole must evaluate the expression 1 - b/(1-b)² and compare his shooting prowess c to the result. If c is better, Cole must shoot in the air, if c is less – aim at Alex. If c happens to be exactly equal, for example b=35% and c=17.1598%, then Cole must decide who he hates more: Alex or Bobby. If Cole shoots in the air first, Alex's survival is (1-b)(1-c), if Cole aims at Alex, Alex's survival chance becomes (1-c)(1-b)(1-c). If Cole hates Alex and Bobby exactly equally, then he must shoot in the air – a noble gesture.
At no time there is any uncertainty, save for the wacky cases c=0, or b=1.

Hopefully, this solves all tiebreak situations and removes the uncertainty.

[Give a monkey enough rope]

Somehow, I see paragraph 2 differently.

I see paragraph 2 this way:

weight = rope + 2*(2*3*3a - 1.125a) -2.25a

When the narrative says "was when," or "will be when,"

denote that time frame by an offset of a, b, c, d ... years.

So "... monkey was years old when (x-a) mother was (y-a)

twice as old as brother was when (z-b) mother was (y-b)

half as old as brother will be when (z-c) brother is (z-c)

three times as old as mother was when (y-d) mother was (y-d)

three times as old as monkey was (x) in paragraph 1.

This says

y-a = 2(z-b)

y-b = (z-c)/2

z-c = 3(y-d)

y-d = 3x

The whole paragraph says W = L/4 + (x-a).

Eliminate a, b, c, d, and use z = (x+y)/2.

That's not what paragraph 2 says in the OP.

[A chessboard]

The stipulation that all 31 rectangles are “of the same size” is still a bit ambiguous. The size could be interpreted as area. If rectangles were equal that would imply they are equal in area (2 squares each) and dimensions. However, do we need a stipulation that rectangles must be alined on square boundaries?

If rectangle's dimensions were specified as 1x2, then the problem would be solved by googon97 in post #5.

But those rectangles could be 1/3 x 6, or 1/2 x 4. Still, it is impossible to cover up the board with 31 of those rectangles.

Furthermore, can we prove that we could or could not cover the board with 31 equal area (2 squares each) rectangles of any dimensions?

[Knight Checker]

It seems hard for White not to win.

1 Nd4xe6 Nc7xe6 (If 1 ... Ne7-c6, 2 Nb4xc6)

2 Nc4-d6 Ne6-g5
3 Nb4-c6

OR
2 ... Ne6-d4
3 Nd6-f7

OR

2 ... Nd7-e5

3 Nb4-a6

If Black had their own tangible threats, that could reduce the number of solutoins to the problem.

[For Bushindo - (others try at your own risk)]

Okay, so earlier we found that not allowing an airshot on Cole's turn reduces to a trivial solution. So, let's assume that on the first shot, Cole has the option of shooting A, B, or none of those two.

We already found that the probability of Cole winning if he shoots at A first is

W_A = (1-p_c)p_c p_b/[ 1 - (1 - p_c)(1-p_b) ] + (1-p_c) (1-p_b) p_c + p_c p_c (1-p_b)/[ 1 - (1 - p_c)(1-p_b) ]

By the same derivation process, we can see the probability of Cole winning if he shoots at the air first is

W_N = p_bp_c/[ 1 - (1-p_b)(1-p_c) ] + (1-p_b) p_c

So, if we set W_N = W_A and solve for p_b and p_c, we see that both strategies are equally beneficial for Cole (hence the uncertainty, I suppose) when

p_c = ( p_b³ - 3p_b + 1)/( p_b-1)²

If it was

p_b² (square instead of cube,) our results would match.

p_c = ( p_b² - 3p_b + 1)/( p_b-1)²

[Knight Checker]

White seems to win in whichever way, provided it has the first move from that position.

1 Nd6

If 1...Ne6 x d4, then 2 Nf7 and both d8 and h8 cannot be defended.

If 1...Ne6-g5 or d8, then 2 Nd4-c6 wins quickly.

If 1 ... Nf6-g4, or any other square, then 2 Nd4 x e6

If 1 ... Nd7-c5 (or to any other square), then 2 Nd4-c6

If 1 ... Nc7-anywhere, then again 2 Nd4 x e6 wins.

Obviously, the Knight on e7 cannot move, since it guards c8.

Also, 1 Nb4-a6 seems to win quickly.

[Mission to Mars!]

I take it in such a way that 4 ships are connected to a 5th ship from 4 sides to give it the energy all the trip ,i.e. only the central ship will be functioning and the others adhering to it are as energy suppliers only.

Your proposal (tethering 4 ships to the 5th) is akin to increasing the mass of the 5th ship by five times while also increasing the fuel tank five times. Your solution assumes that fuel usage for the navigating ship is the same whether it is alone or whether it has 5 times the mass. In physics, as in life, there is no such thing as a free lunch. You can't carry 5 times the mass to Mars without expending extra energy.

Perhaps you are thinking that the navigating ship only has to set a course for the entire fleet, so the energy usage is independent of the mass. Recall that in space, if you need to change the course, you will need to change the momentum vector of the entire fleet. That means if you want to move 1 degree to the left, for example, the navigating ship will need to provide enough thrust (energy) to move its entire mass to the left that much.

Even if we allow the conservation-of-energy violation, the 5 ships still can not make it to Mars and back. From your OP, "each spaceship has a fuel capacity to allow it to fly exactly 1/4 way to Mars" and "Each spaceship must have enough fuel to return safe to the base space station". Since each tank will take you 1/4 of the way to Mars, 5 tanks are enough for 1.25 of the distance to Mars. How are your 5 ships supposed to get to Mars and get home on 5 tanks?

The fuel feeds a small generator on board producing enough electricity to send a signal to Mars' Sub-Ether Tractor Beam station. The signal relays precise position, velocity, and mass of the ships. The Tractor Beam on Mars supplies all required energy and does all the work in pulling and guiding the ships towards their destination.

Once arrived, the ships must bomb the Tractor Beam station, because such is their mission.

You might ask, why Marsians are playing along. Because they know the ship has enough fuel only for a fraction of the distance to send the signal. It's simple.

[For Bushindo - (others try at your own risk)]

I am uncertain, what uncertain means in this context.

Cole's first shot strategy is clear. He must shoot himself in the foot thus exiting the duel with a non-fatal injury. (Hopefully, he does not miss.)

Coles probability to hit the target is

c; Bobby's probability -- is b.
Let's calculate the probability of Cole's survival in one on one duel with Bobby, where Cole shoots first.
X = c + (1-c)(1-b)X
X = c/(b+c-bc)

If Cole's first shot is in the air, Bobby shoots at Alex. If Bobby misses, Alex kills Bobby and Cole has one shot at Alex. If Bobby hits Alex, then a duel between Cole and Bobby ensues with Cole going first. Cole's probability of survival in this scenario is:
(1-b)c + bc/(b+c-bc).
If Cole shoots at Alex and misses, thereafter the probability is the same as as with shooting in the air. If Cole hits Alex, then he has a duel with Bobby shooting first. If survival chances in such duel are worse compared to shooting in the air, it is to Cole's advantage to shoot in the air.
If Bobby misses Cole on his first shot, it becomes a duel with Cole shooting first. Therefore Cole's surviving probability(air shot) > probability(Bobby-Cole duel) is as following:
(1-b)c + bc/(b+c-bc) > (1-b)c/(b+c-bc)

Solving we get:

c > 1 - b/(1-b)²

When b >= 39% the expression yields a negative number, meaning Cole must shoot in the air. For b <= 31% the expression is greater than 31%, which contradicts the condition that Cole is a worse shot than Bobby. That means Cole must try and shoot Alex. For b between 31% and 39%, Cole must carry out calculations and comparison before shooting.

[Colorful cubes]

Actually, we should split the difference and go with 27.

The variation 4 on the diagram in my previous post should have 8 arrangements.

K-man's zig-zag (5) should have 4, instead of 6 variations.
There are 2 different 3-side zig-zags, and each has 2 (not 3) arrangements with the 4th disjointed side.

[Colorful cubes]

Good spacial vision exercise. Without looking at an actual model of a cube, I am not sure I got it right.

Next, let's try it in 4-D.

There are 7 ways in which blue-colored edges of the cube can be conected. And I see the arrangements, which cannot be obtained one from another for each variation as following:

colorcube.gif

So it is 25, unless I missed or duplicated some arrangements.

Correction: It is 10 arrangements for the variation 4.

Then the answer is the same as K-man has found.

[Colorful cubes]

Good spacial vision exercise. Without looking at an actual model of a cube, I am not sure I got it right.

Next, let's try it in 4-D.

There are 7 ways in which blue-colored edges of the cube can be conected. And I see the arrangements, which cannot be obtained one from another for each variation as following:

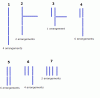
So it is 25, unless I missed or duplicated some arrangements.

[Give a monkey enough rope]

Somehow, I see paragraph 2 differently.

I see paragraph 2 this way:

weight = rope + 2*(2*3*3a - 1.125a) -2.25a

[Give a monkey enough rope]

I understand, it's more of a language exercise, than math.

Let monkey's age in paragraph 1 be

a.
Then from paragraph 3:
Monkey's mother is 4.5a, when monkey is 2.25a.
Then from paragraph 1: a = 16/17 year. And monkey's mother is 3 and 1/17 years old, same as monkey's weight in pounds. So the weight plus the rope are 4 and 10/17 lb.
From paragraph 4: monkey's brother is 1.125a older than monkey and younger than monkey's mother by the same amount. That difference is 18/17 years, making monkey's brother exactly 2 years old in paragraph 1.
From paragraph 2:
Monkey's age calculates as as 31.5a = 29 and 11/17 years old. And by that many pounds the weight exceeds the rope. Whereas together they weigh just over 4.5 lb.