-
Posts
482 -
Joined
-
Last visited
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by HoustonHokie
-
-
ok, I see it now. Needed more coffee, I think (that's twice today I've come up with some oddball stuff). I don't see a way to get more than 1155 cycles for the LCM. The only other primes available other than 11, 7, 5, & 3 are 2, 13, 17, 19 & 23, and they don't appear to help much. And if you have 15.75 * 6 * 60 / 4.5 = 1260 cycles available, you've still got time to get the puzzle written. Of course, it'll be a pain in the rear to log in, which continues to cut into the fishing time.
Of course, I think CL has the solution you'll ultimately adopt if you find yourself in that spot. Lateral thinking is just what we do here...
-
I see some of it now:
Topic: Italy
Alps Venice Primavera Tiramisu Bene
but I've got a couple letters left over (RBT), so something's wrong...
-
Making a couple of assumptions, I think you'd have plenty of time to type the puzzle and go fishing, even on the first day.
Hopefully, the computer is consistent in the outcomes. For example, if you type "B", you always get "G". And, hopefully, if you type "b", you'll get "g", and not something else. If that's the case, then you can solve the puzzle like this:
Assume what the professor was typing was the alphabet: "ABCDEFGHIJKLMNOPQRSTUVWXYZ." And what he got out was the alphabet shifted by one character: "BCDEFGHIJLKLMNOPQRSTUVWXYZA." Then, when he types in "BCDEFGHIJLKLMNOPQRSTUVWXYZA" he'll get "CDEFGHIJLKLMNOPQRSTUVWXYZAB." After 26 such iterations, "ABCDEFGHIJKLMNOPQRSTUVWXYZ" comes out. Each iteration is 4 + 0.5 = 4.5 minutes, and 26 iterations takes 26*4.5 = 117 minutes. The results are probably not a simple shift like this, but something more like a cryptogram, but the principle is the same in that it will only take 26 iterations to get done, assumping simple (consistent) substitution of one character for another.
So, after almost 2 hours of painful computing on the first morning (followed by another couple painful hours online with the outsourced tech support - typing by cryptogram), the professor will make a quick trip to the nearest shipping location, send the laptop off to be repaired, pick up lunch on the way back, and enjoy the rest of his vacation. Hope the fish are biting and your cell phone breaks, to complete the incommunicado plan - the best vacations are the ones where the office cannot get in touch with you

-
It looks like you're suggesting the problem can be boiled down to what happens in the next two rolls of the dice. In two rolls of the dice, Alex has two chances to win (2*1/36), but you only have one (1*1/36). Which would suggest that, overall, Alex is twice as likely to win as you are (p[Alex] = 0.67; p[you] = 0.33). Gotta get a cup of coffee and see if that makes sense when I'm done with it, but it sounds reasonable right now...
Because I made that last post prior to my morning coffee and because I was torn between my logic & Prime's, I decided to do a little simulation to see if I could understand what happens. Using a random number generator in a spreadsheet, I simulated 10000 pairs of rolls of the dice and evaluated whether or not there was a winner in those pairs of rolls. Based on my last post, I expected Alex to win 2/36*10000 = 556 times and me to win 1/36*10000 = 278 times. And that was pretty much what I got. Every time I updated the calcs for the spreadsheet, the numbers regenerated and I got new values for wins, but, in general, Alex was twice as winning as I was. But I was left with a doubt - what about those times when nobody won and a 7 showed up on the second roll? Surely, I was more likely to win on the 3rd roll than Alex was in those cases! Of course, he would still win on other situations that led to a third roll. So, I tried another tactic.
Starting with the same 10000 games, I looked at each roll of the dice individually. After the first roll, Alex should have won 10000/36 or 278 times. I couldn't win in the first roll, but of the remaining 9722 games where the action continues after the first roll, a 7 should appear 10000/6 = 1667 times. So, in round 2, Alex should win 9722/36 times = 270, and I should win 1667/6 times = 278. Now, after (278+270+278 = 826) winners, there are 9174 games still ongoing. And, of those, 9722/6 - 278 = 1342 have a 7 showing. I carried this operation out for 110 rolls, which is the point at which the rounding didn't allow anyone to win any of the 14 remaining games. I found that Alex won 5372 times and I won 4614 times, which is approximately the 7/13 vs 6/13 relationship suggested by Prime (and blew my 1/3, 2/3 thing completely out of the water - like I said, no coffee!). To make sure the rounding didn't affect things too much, I removed it and found that Alex won 5385 times and I won 4615 times, which matches the 7/13 vs 6/13 relationship exactly.
I checked something else, too, just to satisfy my curiosity. It's obvious that Alex's probability of winning on any one roll is constant at 1/36, but I wondered about my probability of winning on a particular roll. So I took the ratio of wins for me to games played (both without rounding) and came up with the following:
Roll 1: p(me) = 0
Roll 2: p(me) = 0.028571
Roll 3: p(me) = 0.024390
Roll 4: p(me) = 0.025018
Roll 5: p(me) = 0.024924
Roll 6: p(me) = 0.024938
Roll 7 (& higher): p(me) = 0.024936
So it looks to me like things are in flux through the first 6 rolls, but even out from 7 on. That suggests some level of dependency at the beginning which turns into independence by the 7th roll, but I haven't figured out why just yet.
-
- The first dice roll is 12 [Alex wins], 7, or x; where x is something else.
- If it's 7, you roll again and get 12 [Alex wins], 7[you win], or x.
- After any x, you're back to square 1.
It looks like you're suggesting the problem can be boiled down to what happens in the next two rolls of the dice. In two rolls of the dice, Alex has two chances to win (2*1/36), but you only have one (1*1/36). Which would suggest that, overall, Alex is twice as likely to win as you are (p[Alex] = 0.67; p[you] = 0.33). Gotta get a cup of coffee and see if that makes sense when I'm done with it, but it sounds reasonable right now...
- The first dice roll is 12 [Alex wins], 7, or x; where x is something else.
-
Assuming the answer to my question #2 above is "no" (ahh, I see the answer now - thanks), I think I can do it in 3 trips around the table. Here's how:
Original: 1 1 1 1 1 1 1 1 1 1 1 1
1st Rev: 0 1 1 2 0 1 1 2 0 1 1 2
2nd Rev: 0 1 0 2 0 2 0 2 0 2 0 2 (only 11 rolls because 1 is in the waiter's hand)
3rd Rev: 0 2 0 2 0 2 0 2 0 2 0 2
-
Clarification request:
1. Does passing a roll over a plate that already has two rolls count as passing over 1 or 2 rolls?
1a. If consecutive plates have 1, 1, & 2 rolls respectively, can a roll be picked up from the first plate and moved beyond the plate with 2 rolls?
2. Does the waiter have to set the roll down on the next plate following the plate with the second roll, or can he keep moving with the roll, provided he does not pass over a third roll? In other words, if you pass over two rolls and the next plate is empty, does the waiter have to set the roll down on the empty plate, or can he move it to a plate that's not empty?
-
Here's how I think about it:
To obtain a 12 is pretty straight-forward. I think everyone agrees that if I roll a pair of dice 36 times, I should expect to see a 12 once.
To obtain two 7s is a little bit different. It requires two rolls of the dice. If I roll two dice twice in a row, I should expect to see two 7s once every 36 times. Seems like the same probability, except for the pair of rolls. I see it like this:
To obtain 12 requires 36 rolls of 2 dice, on average.
To obtain two 7s requires 36 pairs of rolls of 2 dice, on average.
Now pairs of rolls overlap. For example, the first pair is rolls 1 & 2. The second pair is rolls 2 & 3. The third pair is rolls 3 & 4. You get the picture. The 36th pair is rolls 36 & 37.
So, after 36 rolls of the dice, I'll expect to see a 12.
But I'll expect to see two 7s after 37 rolls of the dice.
I don't take the bet.
-
Unless I'm mistaken, the trick is in
of any invidual card. With each successive shuffle, the card will occupy a different position in the deck than it's hadbefore. And it will do so by moving 2 times its current position down in the deck until it becomes part of the bottom of the deck. A card in the bottom part of the deck moves in the opposite manner, in that the distance it moves is based on its position with respect to the bottom of the deck, but it's still a multiple of 2 away from where it was - just in the opposite direction. Looking at the 52 card case and keeping track of the first card looks like this:
1. 1
2. 1*2 = 2
3. 2*2 = 4
4. 4*2 = 8
5. 8*2 = 16
6. 16*2 = 32
7. 32 - (53-32) = 11
8. 11*2 = 22
9. 22*2 = 44
10. 44 - (53-44) = 35
11. 35 - (53-35) = 17
12. 17*2 = 34
And so on. This should work for any size deck. It turns out that each card will occupy every position in the deck exactly once, so the number of perfect shuffles required to return the deck to its original state is equal to the number of cards in the deck.
-
I'm going to put aside the hexagonal packing stuff for a while and try to tackle these proofs.
The finite solution problem is most easily dealt with when the plates are arranged in an n x 1 row on the table initially. And, to further simplify the problem, let's consider that a single plate is on the table. We'll work from there to n x 1, and eventually to any rectangular grid. First, we need to define the maximum table which satisfies the OP conditions.
To start with, let's consider that the table could have any shape. The conditions on placing a second plate require:
1. Not overlapping the first plate, and
2. Not having the center of the new plate off of the table.
The first condition requires the center of the second plate to be at least one radius from the edge of the original plate. The second condition requires the edge of the table to extend to the center of the second plate. Therefore, in order to prevent another plate from being placed on the table, the edge of the table must be less than one plate radius from the edge of the plate. Tracing a path around the edge of the plate exactly one radius away from it's edge defines another circle with a radius equal to twice that of the plate, and also defines the largest table of any shape meeting the OP conditions.
But our table was specified in the OP as being rectangular. So, we need to define the largest rectangle with its furthest edge one radius away from the plate. Any rectangle inscribed in the circular table previously defined will meet these conditions, but the largest such rectangle is actually a square. It's area is 2D units2 and its sides measure √2D. Thus we have defined the largest rectangular table meeting the OP conditions with n=1. Let's call this table the unit table.
To expand to other values of n, let's consider how we might construct a table with n plates. The simplest means of construction would be to place n unit tables side by side in an n x 1 rectangular grid. This would allow for the construction of a table for any value of n, even prime numbers, which become problematic in an a x b grid. But let's check and see if this means of construction is, in fact, creating the largest table meeting the OP conditions for n plates. The means to checking this is to plot the circular boundary conditions for each of the n plates (the circular table) we defined earlier. If the new table is entirely contained within the composite boundary for n plates, we can say it meets the OP conditions. Because each of the individual unit tables is contained within the boundary for the plate it holds and the composite boundary is simply the intersection of multiple individual boundaries, we can say with certainty that the new n x 1 table will be contained within the composite boundary, and the table will meet the OP conditions. But is it the largest such table? Consider what happens if we increase the dimensions. First, consider an increase in the y-direction. An increase in the y-direction can only be accommodated by a corresponding decrease in the x-direction and compression of the plate spacing, or else the table would exceed the composite boundary. Similarly, an increase in the x-direction can only be accommodated by a corresponding decrease in the y-direction and expansion of the plate spacing. Additionally, an increase in the x-dimension is further limited because once the spacing of the plates reaches 2D from center-to-center of adjacent plates, the table will not meet OP conditions. Either dimensional change, even if it results in a table meeting OP conditions, will result in a table with less area than one made of n x 1 unit tables. So we can say that a table made by placing n unit tables side by side defines the maximum table for n plates.
I won't go through it all here, but we can expand this proof for non-prime values of n to show that a table made by placing n unit tables in an a x b rectangular grid (where a and b are factors of n and a x b = n) also creates a maximum table for n plates.
I think this discussion combined with PT's proof of 4 plates covering a unit table proves the general solution is 4n.
As far as the infinite plane/hexagonal packing goes, I think that it may not be relevant any more. My proof above showed that a maximum table can be acheived with an n x 1 arrangement of plates, and so as n approaches infinity, you don't need an infinite plane, but something closer to an infinite line (in that it is bound in one direction but not the other). Hexagonal packing only proves more efficient than square packing in configurations where the plane expands in both the x- and y-directions, so it will never provide the minimum coverage for all tables satisfying the OP conditions.
At HoustonHokie's Hexagonal Hamburgers and Hash, deep in the Heart of Texas, all the tables are hexagons (except for the big circular table in the middle), and the answer might be, well, a little bit different.

-
My reply was directed at bn, who said we still need a proof for 48 plates when he edited the post description.
Yes we do, because we need to make sure that the coverage is the most effecient possible.
In the square arrangement of plates you proposed, each circle effectively covers a square with an area equal to 0.5D units2. There is another way to arrange the plates - like a honeycomb - where each circle effectively covers a hexagon with an area equal to 0.65D units2. On the face of it, that would seem like the better arrangement, because each circle covers more area. But, because they have to be offset from one another instead of stacking horizontally & vertically, some of that efficiency is lost in this particular case. Also, it just happens that the exterior dimensions of the table are multiples of the square arrangement, but not multiples of any of the hexagonal arrangement. But using the hexagonal arrangement is why I can cover the 5.66D by 4.25D table with ony 45 plates. It just doesn't work for the other two possibilities because you end up with partial plates at the edges - at least you do when the plates are oriented "square" with the table. There may be a solution for the other two tables that uses less than 48 with an appropriate rotation. I don't see it yet, but I haven't played with it enough to know for sure. If I can find that, and all other possible tables are smaller than those three, the solution won't be 48 anymore. And that's what bn is driving at with the proof request, I believe...
-
It isn't stated that you should find a maximally inefficient pattern to arrange the plates in the first place.
No, but it is inferred.
The OP gives that 12 plates are on the table and no more can be placed without overlap. Then it asks how many plates are necessary to ensure that the table is covered later on. The ensure part of the OP is what makes us look for the maximally inefficient arrangement. We want to make sure that the waiter can cover the table with plates, no matter what the size, as long as it satisfies the original conditions of the OP (because, of course, the waiter doesn't know the size of tables in his own restaurant
 ).
). I don't want to beat a dead horse, but another way to look at it is like this: The waiter comes to you and says, "I just placed 12 plates on my table and they don't overlap one another and I can't place any more without overlap. Now, I need to cover that table with plates and I don't know how many to order so that I have enough. How many plates do I need?" Being a good problem solver, you tell him, "Well, I don't know the exact dimensions of your table, so I don't know exactly how many you need - it could be anywhere from 12 to 48. So, if you get 48 plates, it will definitely be enough."
That's why I did the problem the way I did.
By the way, you'll notice that I said 12 was the minimum - that's because I've got an arrangement where 12 plates can cover a table that meets the OP requirements. Actually, I have 2 such arrangements.

And I'll throw this out there, too, for what it's worth. That 48 number only stands because the plates are not necessarily arranged in a 3x4 grid. I can cover a 4.25D x 5.66D table with only 45 plates. But I can't do the same for a 2x6 grid or a 1x12 row (yet).
-
Here's my proof:
For the proof, I introduced two new angles, e and f, as follows:
e is the angle opposite side AB on triangle ABP.
f is the angle opposite side AB on triangle ABQ.
By law of sines, we know that:
BQ/sin(a) = AQ/sin(b/2) = AB/sin(f)
BP/sin(a/2) = AP/sin(b) = AB/sin(e)
We also know that:
a/2 + b + e = 180 Þ b + e = 150
a + b/2 + f = 180 Þ b/2 + f = 120
Finally, we are given that:
AQ + BQ = AB + BP
Substituting for AQ, BQ, & BP gives:
AB sin(b/2)__AB sin(a)______AB sin(a/2)
------------- + ----------- = AB + --------------
__sin(f)______sin(f)__________sin(e)
All terms on both sides of the equation include AB, so AB can drop out. Multiplying both sides by sin(e) sin(f) gives:
sin(e) [sin(b/2) + sin(a)] = sin(f) [sin(e) + sin(a/2)]
Substituting for a, e, and f gives:
sin(150 – b) [sin(b/2) + sin(60)] = sin(120 – b/2) [sin(150 – b) + sin(30)]
We now have one equation with one unknown: b.
Solving for b, we get b = 80 and therefore g = 40.
-
Beta = 75 degrees
Gamma = 45 degrees
????
I get AQ+QB < AB+BP with those angles.
-
Perhaps this will help illustrate what we've been saying (I always like a good drawing
 ).
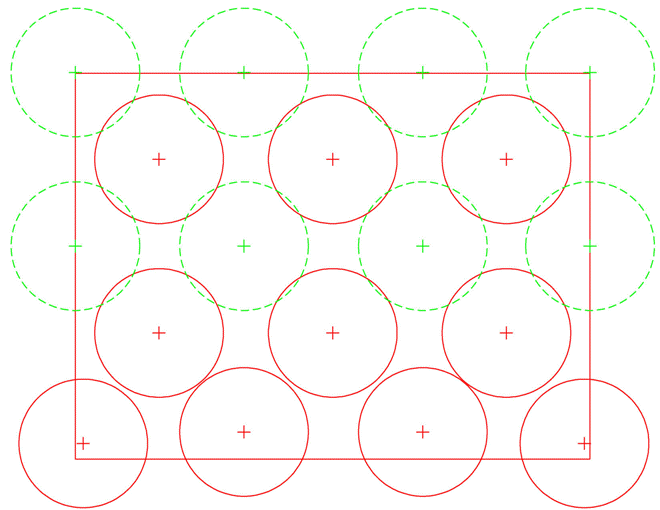
). The image below shows a 3d x 4d table and an arrangement of 10 (red) plates which won't allow for any more. You can see my attempts to add (green) plates which always either overlap another (red) plate or the center of the (green) plate is not on the table. I've spaced the 6 central (red) plates at 1.35D horizontally & vertically, which makes the (green) plates in between overlap. Additionally, I've only allowed 0.17D between the top row of (red) plates and the top edge of the table, which prevents the (green) plates with centers right on the edge of the table from being placed without overlapping that row of (red) plates. [The interplate dimensions could actually be a little larger, but this is easier to see without high image quality.] With this arrangement, there is no way to get an 11th plate on the table, much less 12. So the table has to be enlarged, and PT's & CL's calculations in that regard have been quite helpful in determining the size of the table required. I hope this helps show what we've been trying to say.
-
beta = 80°
gamma = 40°
my proof is messy and lengthy though. I'd like to see the "simple" way to solve this.

Like you, I have a long proof, but I got the same answer. Then I drew it out (as well as the other two solutions that have been posted), and confirmed we're right. I'm looking for that "magic bullet" answer - there always seems to be one

-
I don't understand how you are discussing such a large table. I assume the table dimensions are expressed in terms of plate diameter (not radius).
If your plate has diameter = 1 unit, and the table is 5.5 x 4.3 (or thereabouts), you can get way more than 12 plates on it where they are not overlapping and their centers remain on the table. In fact, you can easily get 30 plates on such a table. In my previous post, I suggested that the size limit (where you can fit 12 such plates but not 13) approaches 3 x 4 d
The area of one plate is pi/4 square units; the area of the table proposed, 24 sq units or so, can easily hold many more than 12, even if you don't take advantage of the fact you are allowed to overhang the edges.
What the heck?
Oh yeah, my answer, 32 is not a multiple of 12!
It's not that you can fit more than 12 plates on such a large table. Of course it's possible to place more than 12 plates on the tables we've been discussing. The nuance we've been looking at is an optimal arrangement of 12 plates on that table such that you cannot add a 13th without either overlapping one of the original 12 or it's center being over the edge. So we've been trying to maximize the spacing between the plates to create the largest table possible where those conditions are not violated. Then, having acheived such a table, we remove the original 12 and see how many plates it takes to cover it completely. The phrasing of the OP (which has been both debated and clarified - thanks, BN), requires us to find the largest table possible to fulfill the 12 plate condition, and the smallest number of plates to cover it completely.
So, you have to do both of the following to solve the puzzle:
1. maximize the size of the table that can have an optimal arrangement of 12 plates, and
2. minimze the number of plates it takes to completely cover it.
I think you'll find that 32 plates are not enough to cover the maximum table.
-
A quick check reveals thatthe table is now 1.41 x 16.97. 4 plates cover 1.41 x 1.41 so we would need 48 plates.48 plates will cover all 3 table sizes: 1.41 x 16.97; 2.83 x 8.49; 4.25 x 5.66. All require exactly 48 plates, so it doesn't matter how the table is sized, except that it conform to the OP requirements - now that we know what they are

-
If the westbound bus leaves NY on day 0, it will encounter every eastbound bus that left SF between days -7 to 7 inclusive, or 15 buses. That assumes that you count the two encounters in the bus stations in NY & SF on days 0 & 7, respectively.
-
Or I could make it a little better...
Now I'm down to 86 plates with an even more optimal arrangement of the plates. Remember I said if...
Note: there are 4 plates in the drawing that violate an OP condition that their centers be on the table. They could be moved so that their centers are on the table and still provide the coverage that necessitates their inclusion in the first place. They would just overlap more...
-
I think the answer
somewhere between 48 and 60. Here's a picture of the optimal covering for four plates. The grey square is sqrt2 by sqrt2 (d=1). Layed out in a rectangle of 4 by 3 squares we could cover a table 5.657 by 4.243. But I think this table could be a little over that and still fit the description of the OP. Of course the OP leaves the size of the table up to us, so maybe we need to find the optimal sized table first.

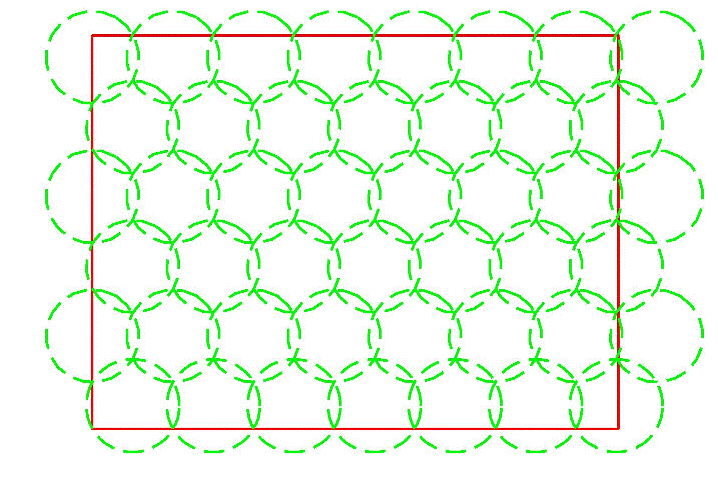
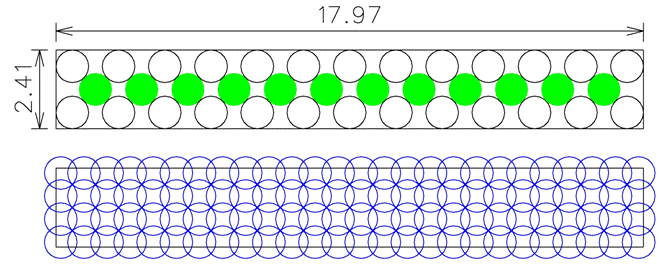
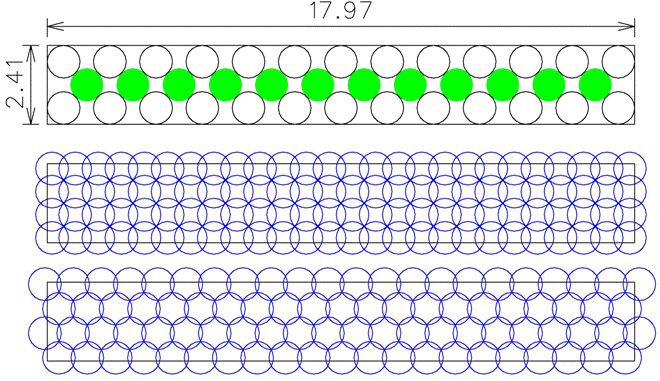
Combining this table size with PT's optimal coverage arrangement, I get:With that in mind, it looks like the biggest table would be2.41 x 17.97, which would allow a single row of plates to be placed at 0.41 between plates and 0.70 from plate to edge. The total area of this arrangement is 43.3, which is larger than the 35.0 achievable with a 5.25 x 6.66 table or the three arrangements I proposed earlier. Now, the question is whether largest area = most plates, or if there could be something in a more compact arrangement that would be more difficult to cover.
104 plates are required to completely cover the 2.41 x 17.97 table. If that's the minimum number of plates needed to cover the maximum size table, the problem is solved. Of course, I said if...
-
Yeah
.7 from plate to edge.
With that in mind, it looks like the biggest table would be
2.41 x 17.97, which would allow a single row of plates to be placed at 0.41 between plates and 0.70 from plate to edge. The total area of this arrangement is 43.3, which is larger than the 35.0 achievable with a 5.25 x 6.66 table or the three arrangements I proposed earlier. Now, the question is whether largest area = most plates, or if there could be something in a more compact arrangement that would be more difficult to cover.
-
is bigger then 3D x 4D. The OP says that twelve plate are on the table and you can't fit anymore on without over-lapping. I had originally thought that meant if the plates were d=1 then the table was just under 9 by 7, but then I realized this would leave room for plates placed in the diagonal between the others. So the table can be just under 4d + 5(sqrt2-1) by 3d + 4(sqrt2-1) or 6.07 by 4.65. Since thats the case, 7 plates (formed like a flower) put in place of each single plate would certainly cover the table. 84 plates, but still it's probably less then that.
I'm questioning your dimensions for the table somewhat. I think I can place 12 plates (dia=1) on a table "just smaller" than 6.5 x 5.33 such that you can't put another plate without overlap, which makes the table a little bigger than what you had. I've also come up with 2 other arrangements of 12.5 x 2.73 and 18.5 x 1.87. They all have similar areas (34.6, 34.1, 34.6). I think these arrangements - particularly the 6.5 x 5.33 - maximize the size of the table we are to cover with plates. If that's right, then we can move on to the minimum number of plates required for complete coverage. You might consider this the first step in the proof we're seeking.
-
Coffee and donut next visit to NY for the lowest provable number.
It's the proof that's so cool.
We're still high on the number, btw.

Re-reading the question, I see that 12 plates already cover the table... I was thinking this was like the last one, and the 12 went along one axis. In that case, I can do it with...
32. It depends a little on how the rectangle is formed, I think.
If D is the diameter of a plate, I can get 32 plates if the rectangle's dimensions are 3D x 4D.
If the dimensions are 2D x 6D, I have to go up to 33 plates.
If the dimensions are 1D x 12D, I get 38 plates.
Donuts?? Or am I still too high?
edit: wait, reading the puzzle again, I think I see what you are looking for is a general solution no matter the what the dimensions are. I'll keep looking


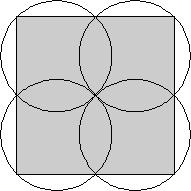
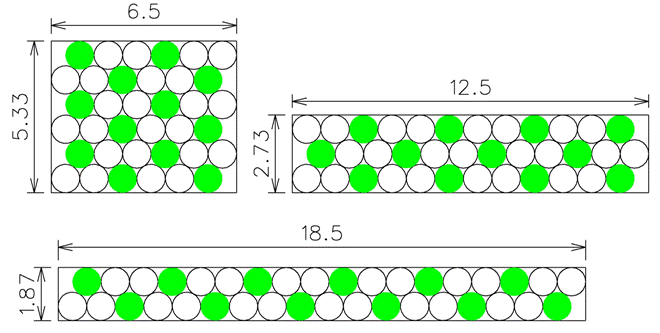
in New Logic/Math Puzzles
Posted
Bonanova's signature keeps taunting me regarding this puzzle, so I had to do some research to see if I could understand some of the basics.