-
Posts
433 -
Joined
-
Last visited
-
Days Won
15
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by rocdocmac
-
-
Spoiler
Using 3x 7 and 1x 0 only(follow-up on my comment to plasmid)
SpoilerRather use flooring! In Excel it will look something like this ... =FLOOR((SQRT(FACT(7)))/7,(7^0))
-
SpoilerOn 8/26/2021 at 5:24 AM, plasmid said:
Rats, I was going to say that ( Sqrt(7!) - 7^0 ) / 7 is close enough that no one's likely to notice the difference.
Just add "ceiling" in front of your equation to get exactly 10!
-
Spoiler
There are 14 solutions to the problem using whole numbers.
If further restrictions are imposed (i.e. all digits are (1) different, (2) all <10, and (3) no zero values), there are two valid answers.
Spoiler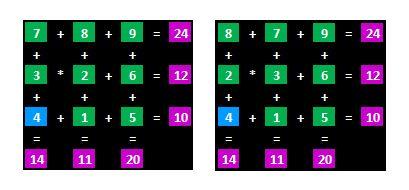
-
Spoiler
10946
(Fibonacci #22)
-
Sent this via email on 30 AprilSpoiler80 started with ...(1) 80-20-10 = 50(2) 50-10-10 = 30(3) 30-15-10 = 5
-
Spoiler
SMALLEST: 529073 64305 + 14745 _______ 608123A=2 C=1 E=4 L=8 N=3 R=7 S=5 T=9 U=0 V=6
ALTERNATIVE:
514038 67805 + 27375 _______ 609218A=1 C=2 E=7 L=9 N=8 R=3 S=5 T=4 U=0 V=6
-
 1
1
-
-
Donald, that's what I thought too!
-
Nothing wrong with the "formula" in red!The distance here is expressed in parsec (pc), where 1 pc ~31 trillion km.
-
For interest's sake, if no true fractions were involved at all, there is an alternative solution ...
Spoilercone = 0; sundae = 42; pink = 31; brown = 11; purple = 5
-
The long way ...
Spoiler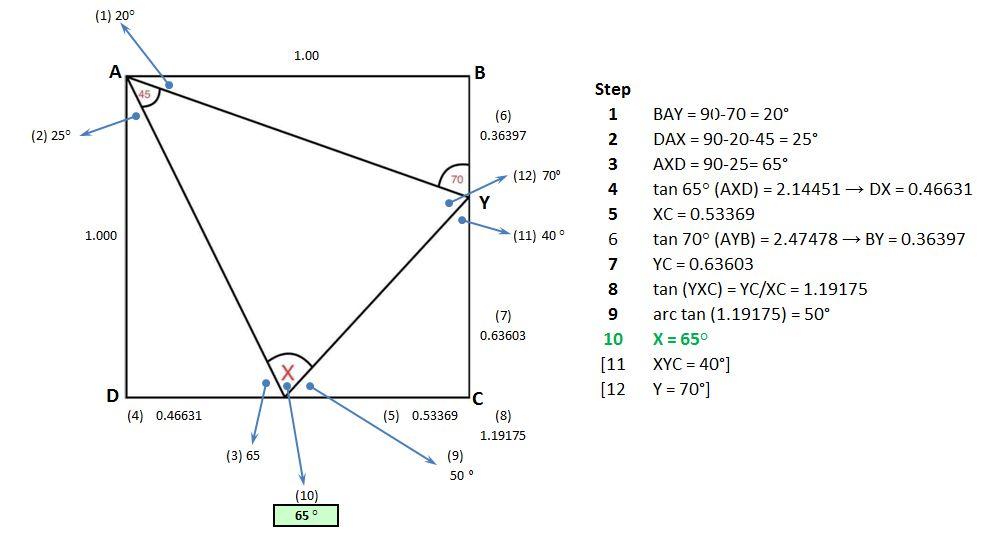
-
YAY!
On 3/19/2020 at 7:45 PM, CaptainEd said:second number: the last digit of powers of 3 runs through the cycle (3971), with exponent divisible by 4 ending in 1. 556677 is 1mod4 so it ends in 3.
second number: the last digit of powers of 3 runs through the cycle (3971)
, with exponent divisible by 4 ending in 1. 556677 is 1mod4 so it ends in 3. -
Spoiler
1 up, 1 down: 50 % again! (still wrong age)
-
Spoiler
You need to revise!
SpoilerIncorrect answer (50 % of digits correct).
-
Earlier today (whilst attending his birthday party) I asked Andy his age, but he said that I can figure that out easily by myself! All I had to do was to add four numbers together.
The first of these four numbers is the last digit in the figure obtained when 2 is raised to the power of 667788 (2667788). Similarly, I had to find the last digit in the evaluation of 3556677, 7445566, and 8334455 to complete the sum.
If today is the 12th of March 2020, when was Andy born?
-
Ah-ha! The first toss is irrelevant. Thus the second player has the best chance ...
SpoilerMy first attempt can then be bettered to 1/3200 rather than 1/6400?
Maximum probability for 2nd player to checkmate would then be then 0.0003125 (~0.03%) on his second move.
But here only for a "2nd to move" win.
If it's a matter of "first to move" to win, then it may look different.
NO - I'm still missing something here ... will start all over!!!!!
-
Spoiler
Probability = 1/(2*20*2*2*20*2) = 1/6400 = 0.00015625 at best along the following line ...
1. Player A (say White) wins first toss (P = 1/2)
2. W moves pawn to f4 (P = 1/20 possible starting moves for W using a pawn or a knight)
3. Player B (say Black) wins 2nd toss (P = 1/2).
4. B moves pawn to e6.
5. W wins 3rd toss (P = 1/2).
6. W moves pawn to g4 (P = 1/20 possible moves = 19 for a pawn or a knight + 1 for K to f2).
7. B wins 4th toss (P = 1/2).
8. B moves Queen to h4.
[Black checkmates on his 2nd move after 4 tosses]
-
Having a stab at this to get the ball rolling ...
Jane Cramer
Janice Carter
Jack Clark
Jasper Clayton
Jim Carver
-
Also thought so, but no! It's in fact 13! Sticking to the method used to generate the next number, of course. But this is where the sequence stops. One can't use the resulting 13-digit number to determine the next one.
-
The five polyominoes chosen with just a single example ...
Spoiler
-
Hint for #1 ...
Spoiler12, 1132 ,? , 11133722, 1113386222, 1111333911222
-
Why no answers? Pretty easy!
-
On 10/4/2019 at 2:34 PM, bonanova said:
In each case is there a swap? Or are there longer cycles as well?
On 10/2/2019 at 6:05 PM, rocdocmac said:In the ten numerical sequences below, three numbers from each sequence have been moved to another sequence, i.e. 15 numbers have been swapped.
Which 15 pairs of numbers should be exchanged to make each of the sequences follow a regular pattern?
(A) 37, 85, 148, 232, 333, 442, 589, 744, 917, 1108, 1317, 1544 (B) 42, 84, 144, 219, 310, 417, 537, 679, 834, 1005, 1208, 1395 (C) 44, 95, 166, 253, 368, 493, 650, 821, 1012, 1223, 1454, 1705 (D) 70, 122, 189, 271, 366, 475, 598, 735, 890, 1051, 1230, 1423 (E) 123, 181, 252, 335, 430, 540, 656, 787, 930, 1085, 1283, 1431 (F) 149, 209, 280, 361, 452, 553, 691, 785, 916, 1057, 1192, 1369 (G) 160, 190, 220, 253, 288, 325, 364, 406, 448, 499, 540, 589 (H) 253, 320, 395, 478, 569, 666, 775, 886, 1013, 1144, 1252, 1430 (I) 257, 300, 351, 405, 465, 528, 595, 668, 741, 820, 903, 990 (J) 306, 371, 452, 519, 602, 664, 786, 887, 994, 1107, 1226, 1351 Example
In the two sequences below, 48 and 52 should be swapped to make sense (A5 ↔ B4).
(A) 20, 25, 32, 41, 48, 65. 80
(B) 15, 24, 35, 52, 63, 80, 99
I wish to point out a trivial mistake in my OP ...
The value at position C10 (1223) and the one at J11 (1226) have inadvertently not been swapped before posting, So both these values are in their correct placings.
This means that only 14 swaps need to be done.
No extra cycles, all straightforward X ↔ Y (one exchange per number with another).
-
In the ten numerical sequences below, three numbers from each sequence have been moved to another sequence, i.e. 15 numbers have been swapped.
Which 15 pairs of numbers should be exchanged to make each of the sequences follow a regular pattern?
(A) 37, 85, 148, 232, 333, 442, 589, 744, 917, 1108, 1317, 1544 (B) 42, 84, 144, 219, 310, 417, 537, 679, 834, 1005, 1208, 1395 (C) 44, 95, 166, 253, 368, 493, 650, 821, 1012, 1223, 1454, 1705 (D) 70, 122, 189, 271, 366, 475, 598, 735, 890, 1051, 1230, 1423 (E) 123, 181, 252, 335, 430, 540, 656, 787, 930, 1085, 1283, 1431 (F) 149, 209, 280, 361, 452, 553, 691, 785, 916, 1057, 1192, 1369 (G) 160, 190, 220, 253, 288, 325, 364, 406, 448, 499, 540, 589 (H) 253, 320, 395, 478, 569, 666, 775, 886, 1013, 1144, 1252, 1430 (I) 257, 300, 351, 405, 465, 528, 595, 668, 741, 820, 903, 990 (J) 306, 371, 452, 519, 602, 664, 786, 887, 994, 1107, 1226, 1351 Example
In the two sequences below, 48 and 52 should be swapped to make sense (A5 ↔ B4).
(A) 20, 25, 32, 41, 48, 65. 80
(B) 15, 24, 35, 52, 63, 80, 99
-
Spoiler
I + VIII = IX


Solve This Riddle And Message Me The Answer And I Will Give Everyone Free 1 Year Netflix Subscription If You Are From US
in New Logic/Math Puzzles
Posted · Edited by rocdocmac
He was born in a hospital ...
... in room number 1995