[Connect the Dots]

Total length = 6 * sqrt 2 = 7.414

Spoiler

 

 

[nazi numbers]

7 hours ago, jhawk said:

First of all you don't proofread your typing,if you go right or left A cells, go up or down B cells

  Hide contents

  Hide contents

your cell number is X*Y  each or the 4 numbers generated will be ( X+A ) ,or (X-A) ,times (Y+B), or (Y-B).  Add the 4 numbers and you get 4XY

 

 

sorry if my words is confusing.
I mean go right (or left) from last position.

your answer is close but still wrong.
If I draw from your answer, the shape will be a rectangular on a flat surface.
 _______
|       |
|   x   |
|_______|

[nazi numbers]

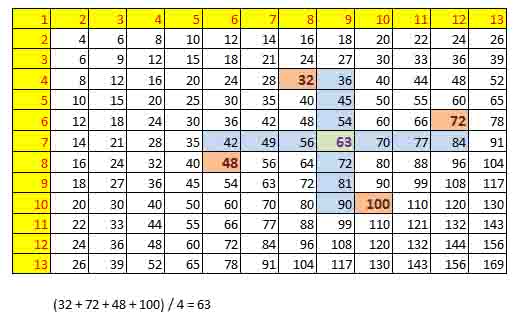
create a m x n table.
then put the multiplication result of x,y coordinate in each cell.

set any cell as your preffered base.
from the base go up    A steps, then go right (or left) B steps, take the number as num1
from the base go left  A steps, then go right (or left) B steps, take the number as num2
from the base go down  A steps, then go right (or left) B steps, take the number as num3
from the base go right A steps, then go right (or left) B steps, take the number as num4

(num1 + num2 + num3 + num4) / 4 = your number.

anybody can explain this ?

[Letter/Number Puzzles : BRAIN * DEN = .....]

Find the digit that each letter represents in the equation MAD * MATH = BRAIN * DEN.

[recursive sequence]

look at this interesting sequence :

 a = 2+1 = 3
 b = 2(a)+1 = 7
 c = 2(b)+1 = 15
 d = 2(c)+1 = 31
 e = 2(d)+1 = 63
 f = 2(e)+1 = 127 and so on

the sequence follow this rule 2⁽ⁿ⁺¹⁾-1

prove it !

[Hat guess the number]

On 2/18/2016 at 7:33 PM, sujith said:

How and why

 

B: see 4, there are 2 possibility : 1 x 4 or 2 x 2. so B do not know the 2 numbers
   so B first say "No"

A: see 5, there are 2 possibility : 1 + 4 or 2 + 3.
   From B answer, A still can't deduce the 2 numbers.
   if B see 6 (2*3) B will say No (2 possibility 1*6,2*3)
   if B see 4 (1*4) B will say No (2 possibility 1*4,2*2)
   so A say "No"

B: From A answer
   if A see 4 from (2*2) there are 2 possibility : 1 + 3 or 2 + 2.
   but A must say yes, because if the numbers are 1 and 3, B will answer "yes" imediately
   so A must deduce the numbers are 2 and 2 in the first try.

  So A must be see 5, and B deduce the numbers must be 1 and 4

[rang the bell.]

I was inactive for 4 days.

@TimeSpaceLightForce

Using time is the right answer, but they don't need that long. If they can measure the time accurately, both using accurate watch, the first man can inform the number not more than 2 minute.

 

[rang the bell.]

Ok, maybe my question is not specific enough.

- There is only one room, not hotel.
- The man inside the room, is giving information to his friend outside the room, by pushing the bell button once.
- there is only 1 bell, and it just ring, not stated something.
- The man inside the room, can't control how long the bel ring.
- the number is between 0 and 100.

[star]

13 hours ago, Logophobic said:

1+6+9+5+12 = 5+12+10+4+2, as required: A+B+C+D+E = D+E+F+G+H

Of course, A+B+C+D+E = F+G+H+I+J does seem more appropriate, but I was working with what you posted.

Ok, I just realize my question was wrong, yes it should be A+B+C+D+E = F+G+H+I+J 

[rang the bell.]

A man enter a room. In the room there is a 2 digits number on the wall.
His friend outside the room do not know the number.
But just by ring the bell once, his friend know the number.
how could this happen ?

[star]

 

9 hours ago, Logophobic said:

 

Very good start, your second answer is right, 
but the first answer is wrong, because 1+6+9+5+12 =/= 10+4+2+8+3.

We can easily find the other right answer from the first right answer.
use your second answer to find another right answer (ofcourse without rotation and reflection)
hint : put the inner points to the outer points.

 

[we are paradox]

I think, "conservation of mass and energy" law is a paradox.

Because if mass and energy can't be created, 
then you and me should not exist.

[star]

Put numbers 1,2,3,4,5,6,8,9,10,12 each point, so :
- The sum of points in every line  are equal,
- A+B+C+D+E = D+E+F+G+H

There are 2 solutions.  
(Rotation and Reflection are considered as 1 same solution)

[Hat guess the number]

B : No
A : No
B : Yes

Spoiler

 

B: see 4, there are 2 possibility : 1 x 4 or 2 x 2. so B do not know the 2 numbers
   so B first say "No"

A: see 5, there are 2 possibility : 1 + 4 or 2 + 3.
   From B answer, A still can't deduce the 2 numbers.
   if B see 6 (2*3) B will say No (2 possibility 1*6,2*3)
   if B see 4 (1*4) B will say No (2 possibility 1*4,2*2)
   so A say "No"

B: From A answer
   if A see 4 from (2*2) there are 2 possibility : 1 + 3 or 2 + 2.
   but A must say yes, because if the numbers are 1 and 3, B will answer "yes" imediately
   so A must deduce the numbers are 2 and 2 in the first try.

  So A must be see 5, and B deduce the numbers must be 1 and 4

 

 

[my age]

Some more years, I will turned  x years of age in the year x².
How old I'm now ? (I'm not using miraculous anti-aging treatment now.)

[check digit problem]

@bonanova. How do you get the numbers?

 

My answer is very close to your answer for 6 digits numbers. 

If I search the numbers by computer start from 000000 to 999999 the result is exactly same with your calculation. (although maybe it is not the best answer)

 

["000000","011111","022222","033333","044444","055555","066666","077777","088888","099999","101234","110325","123016", "132107","145670","154761","167452","176543","202318","213209","220153","231042","246735","257624","264580","275491","303145","312054", "321360","330271","347506","356417","365723","374632","404826","415937","428405","439514","480649","491758","506951","517840","529687","538796", "581473","590562","608579","619468","626894","637985","684257","695346","724978","735869","748021","759130","786302","797213","842963", "853872","962831","973920"]

[check digit problem]

Find the maximum number of distinct ways you can create combination of six digit number
(from 0 through 9). with following rules :

1. Each number can be used more than one. 
2. Any two combinations can have at most 1 digit in same place.

example :
a. 075922 and 166433 is accepted.
b. 075922 and 166432 is accepted, both put 2 in 6th place).

c. 075922 and 066432 cannot both be used,
   because both put 0 in first place, and 2 in 6th place).
 

[A Complicated Numbers Problem]

I think I have found the answer

Spoiler

 

I just found intersting connection 

(a+b)⁵ + (a-b)⁵ =  (a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵ ) + (a⁵ - 5a⁴b + 10a³b² - 10a²b³ + 5ab⁴ - b⁵ ) = 2a⁵ + 20a³b² + 10ab⁴

there you don't have to count odd exponent of b. 

after I tried it in haskell,  (3 + √5)ⁿ  + (3 - √5)ⁿ  is very close with (3 + √5)ⁿ

so just count (3 + √5)ⁿ  + (3 - √5)^n, with above ways and substract the value with 1. 

example : 

(3 + √5)⁴ = 751.6594202199647

(3 + √5)⁴  + (3 - √5)⁴ = 752

 

(3 + √5)⁵ = 3935.739820199815

(3 + √5)⁵  + (3 - √5)⁵ =  3936

 

 

[A Complicated Numbers Problem]

First count (sqrt 5), in very high precision.

Then use pascal triangle formula.

then group every odd exponent of sqrt (5). then multiple it by (sqrt 5) just once, you will get right answer.

you will get better precision.

example

(a+b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

         = a⁵ + b(5a⁴ + 10a²b² +b⁴) + 10a³b² + 5ab⁴

(3 + √5)⁵ = 3⁵ + √5(5.3⁴ + 10.3^2.5 + 25) + 10.3^3.5+ 5.3.25 = 1968 + √5*880 

[three circles]

Solution :

Spoiler

 

I call it Another "Easy" Puzzle, because it have a strong connection with my first question (Easy Puzzle).

use solution from my first answer :  A = 1, B = 5, C = 6, D = 3, E = 2, F = 7

then write it like this :A = 2¹ , B = 2⁵ , C = 2⁶ , D = 2³ , E = 2² , F = 2⁷

so (A,B,C,D,E,F) = (2,32,64,8,4,128)

This works by the Exponent Laws: x^m * xⁿ = x^m+n

 

 

[Gold Bar on a Bus]

Ask the bank's guard to take the gold bar for you, then you can go to the bank by bus.

    or ask someone else to take the gold bar for you, then you can go to the bank by bus. They can bring the gold bar by other vehicle.

[three circles]

1st hint : all the numbers are 2 raised to the power of something. (2 = 2¹, 4 = 2², 8 = 2^3, 32 = 2⁴)

2nd hint : Use exponent laws

Exponent Laws: 

x^m * xⁿ = x^m+n

[liar and truth-teller]

You meet 4 persons, at least one of them always tell the truth, and the other always lie.

Then you have conversation with them.

Andre  : I, Brian and Cole are truth-tellers, Diego is a liar.
Brian  : I'm truth-teller, Andre and Cole are liars.
Cole   : I, and Andre are truth-tellers, other are liars.
Diego  : I, and Andre are truth-tellers, Brian is a liar.

Identify the liars and truth-tellers.

[three circles]

hint : all the numbers are power of 2. 

[three circles]

Another "Easy" Puzzle

Find The value of x and y, then put numbers 2,4,8,32,x,y to each point, so :

I.  The product of points in every circle  are equal,  (A*E*F*C = B*E*D*C = A*D*F*B)
II.  A*B*C = D*E*F

There are 2 solutions (Reflection and rotation solutions are considered as 1 same solution)