
karthickgururaj
-
Posts
91 -
Joined
-
Last visited
-
Days Won
2
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by karthickgururaj
-
-
For a finite set, like A = {1, 2, 3}, clearly the super set has higher number of elements (in this case 8), so we can't define an injection from the superset to the original set.@karthickgururaj,
S-B theorem seems to be exactly what we're looking for.
The part that seems difficult, but I can't yet say it's impossible, is the injection from the superset into the original set.
In your solution, can you identify (or give examples of) sets A and B? That would complete the proof.
Or, apply it to say A = {1, 2, 3}.
For an infinite set, like N = {1, 2, 3, .. }, it is not immediately clear whether we can (or not) define the injection from the superset of N (lets call it S(N)) to N.
(So, I have just restated part of the OP!)
S(N) will be like, { {1}, {2}, {1, 2, 3, 100}, {4, 5, 6}, {10^9, 10^8, 10^7}, ... }. Specifically, the assumption here is that the super set does NOT have an element like: {2, 4, 6, 8, ...}.
Then, any specific element of S(N) will have a finite set of elements: {x0, x1, .., xn}. This can be mapped to a unique number in N: : p(x0)*p(x1)*..*p(xn), where p(m) denotes the mth prime number (p(1) = 2, p(2) = 3, etc).
However, I do not know if the assumption is valid. After reading about Cantor's theorem, it appears not.
-
@plasmid, With the givens, I do not believe {2, 2Π, 4 - Π} satisfy the three reals.
Substituting your three reals into the equation
a(2) + b(2Π) + c(4 - Π) = 0
...then solving for Π as if it were a variable results in the following equation, which implies that Π would not be trancendental or irrational given a, b, and c are integers:
Π = (2a + 4c)/(1 - 2b)
(1-2b) != 0
This is an interesting puzzle..

-
The set of all subsets of a set S is called a power set (powerset) of S.
According to Cantor's theorem, cardinality of the power set of any set S
is strictly greater then cardinality of S.
PS The Schröder–Bernstein theorem was called Cantor–Bernstein theorem at my set theory classes.
Interesting! Thanks for the link. Reading the wiki article exposes one assumption in my solution. I assumed that, while the super set has infinite number of elements, each individual element of the super set has a finite number of elements. In other words, I assumed that (for example), "the set of all even numbers" is NOT a member of super set.
If that assumption is removed, my solution won't work.
-
See if there's a similar case (of oppositely directed injections) that applies to finite sets.
For finite sets it is easy to see that a bijection exists, if there are two injections, one from A to B, and other from B to A.
If f: A -> B is an injection from A to B and g: B -> A is an other injection from B to A, then the number of elements in A and B are both same. So, a bijection can be defined from A to B.
I googled a bit on this and read about Schröder–Bernstein theorem, which essentially asserts that if there are two injections in reverse directions, then a bijection exists.
-
I think I got this.. pleased as punch

Let, N be the set of counting numbers, {1, 2, 3, ..}. Let S(N) be its super set.
The one-to-one mapping from N -> S(N) is easy, for each 'x' in N, we map it to {x} in S(N).
For the mapping S(N) -> N, take any element {x0, x1, .., xn} in set S(N). Map it to: p(x0)*p(x1)*..*p(xn), where p(m) denotes the mth prime number (p(1) = 2, p(2) = 3, etc). This maps each element in S(N) to a unique element in N.
karthikgururaj proposes two injections (both of which are far from being surjections also) rather than a single bijection.
So the question is, are two (one each direction) injections equivalent to a bijection?
I thought about this when posting the solution.. In truth, it doesn't appear to be an equivalent to bijection
If an injection can be defined from set A to B, then it implies cardinality of B must be greater than or equal to A. If an injection can be defined both ways, it implies the cardinality of both must be same.. This is trivial for finite sets, I'm not sure for infinite sets.
-
no you can't
if you could, you could map the counting numbers to the reals, which are uncountably infinite.
to prove this, simply let each subset represent a decimal number, with the decimal point after the first number in the set, and the rest of the number in the set of the remaining numbers.
for example the subset {1, 3, 5, 7, 11, 13...} would be represented as 1.3571113...
to prove that the real numbers are uncountably infinite, imagine you try to construct a countably infinite number of real numbers.
say the following list. 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.01 ... now i will construct a number not on the list. take the digit in each decimal place, add 1 unless 9, then go back to 0. so for the above sequence, the number 2.21111... will never appear.
Since the subset is unordered, a single subset can map to more than one decimal number. For example, {1, 3, 5, 7, 11, 13} can map to either 1.3571113 or 3.5171113 or 7.1113531 or.. etc. So it is one-to-many mapping, not one-to-one.
Further, a given subset will represent only a rational number. Irrationals will require mapping of subset with infinite number of elements - which is not legal.
-
I think I got this.. pleased as punch

Let, N be the set of counting numbers, {1, 2, 3, ..}. Let S(N) be its super set.
The one-to-one mapping from N -> S(N) is easy, for each 'x' in N, we map it to {x} in S(N).
For the mapping S(N) -> N, take any element {x0, x1, .., xn} in set S(N). Map it to: p(x0)*p(x1)*..*p(xn), where p(m) denotes the mth prime number (p(1) = 2, p(2) = 3, etc). This maps each element in S(N) to a unique element in N. -
This is only an issue for Bob; he needs Karthikgururaj's suggestion of a rolling start.
For Alice, it's not a problem; she only needs to slow to a momentary stop at the integer mile markers.
She can still win. Her peak speed for the first .2 miles of every lap would just need to be a little greater.
I agree - I was wrong in my earlier post. The diagram in particular has a big mistake.
It looks like Alice has to change her speed instantaneously, at 0.2 mile mark
-
Let s(t) be the distance Alice covers in time 't'.
We assume s(t) is a continuous and differentiable function of 't' - a reasonable assumption: Since Alice can't disappear and appear in a different spot in zero time (implying infinite speed), and can't instantaneously change her speed to a completely different value (implying infinite acceleration).
This is exactly what meant by the last sentence of my answer:
The question remains: is it possible to run like this?
Ok - I misunderstood then.
I'd also add one more condition: s(0)=0, since the runners start moving when the the race starts.
Same restrictions should also apply to Bob,
Agree!
so another question is: how can he run with a constant positive speed?
Obviously he can't without braking his speed function at 0.
True
 I didn't bring that up.. but one possibility is to do a "rolling start", starting from behind the race line.
I didn't bring that up.. but one possibility is to do a "rolling start", starting from behind the race line.Annotated my comments above..
-
A graphical approach..Alice could run fast for 0.2 mile then slow for the rest of the first mile,
and repeat this pattern for the whole marathon.
This way her pace is constant on every 1-mile segment.
Now, after 26 miles of the race she is 26 seconds behind Bob,
and she is going to run fast on remaining 0.2 mile segment of the race.
If she runs fast enough the fast segments, she wins.
The question remains: is it possible to run like this?
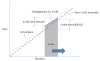
The dashed slanted line represents a constant pace of 8:01 min/mile. The red-dashed line represents a possible pace Alice ran at.
Now, select any two points on the "distance" axis, separated by equivalent of 1 mile unit. Draw verticals as shown to intersect both the pace lines. Draw a line that connects the point where the verticals meet the red-dashed lines. This line represents the average pace for Alice for that one mile.
Now, the requirement is that the average pace should be equal to 8:01 min/mile. Which means, the average pace line is parallel to the 8:01 min/mile pace line.
Further, if we slide the 1-mile window (left or right), the average pace line must still be parallel to the 8:01 min/mile pace line.
Without proving formally, I assert that is possible iff the red-dashed line is exactly same as the 8:01 min/mile pace line.
Let s(t) be the distance Alice covers in time 't'.
We assume s(t) is a continuous and differentiable function of 't' - a reasonable assumption: Since Alice can't disappear and appear in a different spot in zero time (implying infinite speed), and can't instantaneously change her speed to a completely different value (implying infinite acceleration). It is ok for her to cover a large distance (say 20 miles) in a small fraction of a second (say, 10-100).
We further assume that s(t) is increasing function of t. In other words, if x > y, then s(x) >= s(y). Basically, Alice doesn't start running backwards.
Obviously, we stick to a universe governed by classical/Newtonian mechanics and where time flows continuously
Let,
N = 1 mile
M = 26.2 miles
T = 8:02 minutes
Ta = Time Alice takes to complete the race
s(t) = M for t > Ta, but we don't bother about what happens after the race.
As per the OP, the following assertion is true:
If,
s(x) - s(y) = N,
then,
x - y = T, for any s(x), s(y) < M (or equivalently, for x, y < Ta).
We first note that the converse is also true: In every 8:02 minute interval during the race, she covers 1 mile. Because: 1. if there is a 8:02 minute interval in which she covers more than 1 mile, then there is a 1 mile distance that she does in less than 8:02 minutes 2. if there is a 8:02 minute interval in which she covers less than 1 mile, continue ticking the clock until she covers one mile - and note that she has taken more than 8:02 minutes for covering that one mile.
So,
s(t + T) - s(t) = N, if (t+T) < Ta and t > 0.
and/or,
s(t) - s(t - T) = N, if t < Ta and t > T
For any time 't' during the race, at least one of the conditions above will hold true.
Increasing time by 'dt', we get
s(t + T + dt) - s(t+dt) = N
and/or,
s(t + dt) - s(t - T + dt) = N
Subtracting from earlier equation, we get:
s(t+T+dt) - s(t+T) = s(d+dt) - s(t)
and/or,
s(t-T+dt) - s(t-T) = s(d+dt) - s(t)
If,
ds = Incremental change in 's' at time t,
then from equation above,
ds = s(t+T+dt) - s(t+T)
and/or
ds = s(t-T+dt) - s(t-T)
So the rate of change of speed (= velocity here) at any arbitrary point 't' must equal
a. The velocity after time T (if race is still in progress after time T)
b. The velocity that was before T (if race had started by then)
Since 't' is any arbitrary point of time during the race, the conditions above is only possible if the velocity is constant through out the race.
-
What is the most efficient way to time a 15-second interval using a 7-second and an 11-second hourglass?
Start both together. As soon as 7-sec hour-glass ends, 15-sec interval starts. When 11-sec hour-glass ends, flip it over. When it ends again, 15 secs are over.
-
I think with that hint and plasmid's earlier work, the solution seems easy..consider employing the euclidean algorithm instead.
[spoiler start of proof]
If two of the ai vanish, say a2 and a3, then r1 must be zero and we are done.
Assume at most one ai vanishes. If any one ai vanishes, say a3, then r2/r1 = −a1/a2 is a nonnegative rational number. Write this number in lowest terms as p/q, and put r = r2/p = r1/q. We can then write r1 = qr and r2 = pr. Performing the Euclidean algorithm on r1 and r2 will ultimately leave r and 0 on the blackboard. Thus we are done again.
.... more cases to consider
If r1/r2 is a rational, where r1 and r2 are real, then the Euclidean algorithm will terminate in finite steps.
And with the original constraint on r1, r2 and r3, it is easy to prove that r1/r2, r2/r3 and r3/r1 are all rational.
I take back the second statement

Let a and b be two positive integers, (a>b). We form a new pair, a', b', such that, a' = b, b' = a - q0.b (q0 is a positive integer), and a'>b'. If b' == 0, the process stops; else we continue the same way to construct a'' and b'', and so on.
The following assertions can be easily proven: The process above will terminate in finite steps. This is essentially the Euclidean algorithm.
Now, let ra and rb be two real positive numbers (not necessarily rational) such that, ra/rb = a/b. We can now form a new pair, ra', rb' from a', b' and q0 (where a', b' and q0 retain the meaning as earlier) such that, ra' = rb, rb' = ra' - q0.rb. It is easy to show that ra'/rb' = a'/b'. For every step in the process earlier, we can form a new pair with the real numbers, ultimately reducing one of the numbers in the pair to zero in finite steps.
-
inspired by bonanova's puzzle, here's mine.
there are three boxes each containing a prime. it is known that the largest of the three is no more than twice the size of the smallest. (so 7, 11, 13 is the smallest possible values for the three boxes.)
you open one box, and must guess whether your number is smaller, larger or in between the other two values.
which should you guess?
One can enumerate the possible options after seeing the number in the first box?
For example, say the number in the first box is 31.
If 31 is to be the smallest of the lot, then the largest can be max 61 and min 41, so we have the following possibilities:
If largest is 41: (31, 37, 41) -> 1 possibility
...
If largest is 61: (31, 37 or 41 or 43 or 47 or 53 or 59 , 61) -> 6 possibilities.
The total number of possibilities is: 1 + 2 + 3 + 4 + 5 + 6 = 21.
Or in general,
1. If p1 is the number in the first box
2. Let p2, p3, etc be the next prime numbers that occur in the integer sequence after p1.
2. Let pn be the highest prime that is less than 2*p1
3. The number of possibilities where p1 happens to be the smallest is: (n-2)*(n-1)/2
Next, if the number is to be the middle prime, again taking 31 as an example, the possible values are:
(19 or 23 or 29, 31, 37) -> 3 possibilities
(23 or 29, 31, 41) -> 2 possibilities
(23 or 29, 31, 43) -> 2 possibilities
(29, 31, 47) -> 1 possibility
(29, 31, 53) -> 1 possibility
Total: 9 possibilities.
Slightly harder to express this in general terms..
Finally, if the number is to be the largest, then we have the following possible triplets:
(17 or 19 or 23, 29, 31) -> 3 possibilities
(17 or 19, 23, 31) -> 2 possibilities
(17, 19, 31) -> 1 possibilities
Total: 1 + 2 + 3 = 6 possibilities.Just like the first case (where p1 was to be the smallest), it can be expressed in slightly more general terms..1. If p1 is the number in the first box
2. Let p2, p3, etc be the previous prime numbers that occur in the integer sequence before p1.
2. Let pn be the lowest prime that is greater than p1/2
3. The number of possibilities where p1 happens to be the largest is: (n-2)*(n-1)/2
We can go with the choice with the largest number of possibilities.. -
[spoiler='Demonstration for irrational case']Amazingly, everything is on the Web.
This guy used Mathematica to simulate the problem.
For 185 degrees, it takes 4 cuts.
For 1 radian (an irrational number) it takes 84 cuts.
Thanks for the link! Upvoted

-
consider employing the euclidean algorithm instead.
If two of the ai vanish, say a2 and a3, then r1 must be zero and we are done.Assume at most one ai vanishes. If any one ai vanishes, say a3, then r2/r1 = −a1/a2 is a nonnegative rational number. Write this number in lowest terms as p/q, and put r = r2/p = r1/q. We can then write r1 = qr and r2 = pr. Performing the Euclidean algorithm on r1 and r2 will ultimately leave r and 0 on the blackboard. Thus we are done again..... more cases to considerI think with that hint and plasmid's earlier work, the solution seems easy..
If r1/r2 is a rational, where r1 and r2 are real, then the Euclidean algorithm will terminate in finite steps.
And with the original constraint on r1, r2 and r3, it is easy to prove that r1/r2, r2/r3 and r3/r1 are all rational.
-
Alice could run fast for 0.2 mile then slow for the rest of the first mile,
and repeat this pattern for the whole marathon.
This way her pace is constant on every 1-mile segment.
Now, after 26 miles of the race she is 26 seconds behind Bob,
and she is going to run fast on remaining 0.2 mile segment of the race.
If she runs fast enough the fast segments, she wins.
The question remains: is it possible to run like this?
A graphical approach..
The dashed slanted line represents a constant pace of 8:01 min/mile. The red-dashed line represents a possible pace Alice ran at.
Now, select any two points on the "distance" axis, separated by equivalent of 1 mile unit. Draw verticals as shown to intersect both the pace lines. Draw a line that connects the point where the verticals meet the red-dashed lines. This line represents the average pace for Alice for that one mile.
Now, the requirement is that the average pace should be equal to 8:01 min/mile. Which means, the average pace line is parallel to the 8:01 min/mile pace line.
Further, if we slide the 1-mile window (left or right), the average pace line must still be parallel to the 8:01 min/mile pace line.
Without proving formally, I assert that is possible iff the red-dashed line is exactly same as the 8:01 min/mile pace line.
-
Alice and Bob run a standard 26.2-mile marathon race.
Bob's pace is a constant 8 minutes/mile, start to finish.
Alice's pace is such that for every 1-mile segment of the race, she takes 8:01 minutes.
That is, between mile markers 10 and 11, Alice consumes 8:01 minutes.
And between miles 6.374 and 7.374, Alice consumes 8:01 minutes.
Is Bob the sure winner of the marathon?
I think, yes.
The pace can be 8:01 for every 1-mile segment if and only if it is a constant pace of 8:01 min/mile.. I think

-
I would agree with gavinksong that...
...the best way to bet with Bob would be to guess the mode, which with the number distribution that was shown would be 9.
For Alice, you would have to look at the actual distribution and, for each number, count out how many times you see a number appear within any given margin.
The distribution is:
1: 3
2: 1
3: 2
4: 2
5: 0
6: 3
7: 0
8: 1
9: 5
The optimal guesses if you knew the error margin would be
Error margin 1: either 8 or 2 (both had 6 hits within +/- 1)
Error margin 2: either 7 or 8 (9 hits within +/- 2)
Error margin 3: 6 (13 hits)
Error margin 4 or greater: 5 (everything)
If you have absolutely no idea what Alice's error margin is, then you can't give a definite answer. If you know the error margin is likely to be either 1 or 2, then go with 8.
Thanks, this is interesting

I agree with you on the answer to be given to Bob. This would be 9.
I understand your approach.
But the integer closest to mean (or the "expected" value) turns out to be 5, which the last choice in your argument.
(Actually, I constructed the list of samples with the intent of keeping the expected value to be exactly 5, with the number of samples as 18, totaling to 90. But I see now that I made some mistake and hence the number of samples have become 17, yielding expected value as ~ 5.3. Fortunately, doesn't affect the results drastically - the closest integer is still 5 at least).
The S.D for the samples turns out to be ~ 3.1378, yielding SEM to be: 3.1378/sqrt(17) = 0.761.
Question is: Should mean be used or should Charlie go with your analysis..?
I'm going to agree with plasmid here.
The expected value of 5 makes sense if you assume a uniform probability distribution. Not knowing the distribution one cannot calculate the expected value. For all we know, the machine may be programmed to never (or extremely rarely) produce a 5. Deriving the possible distribution from the sample is your best bet, which is exactly what plasmid did.
While I'm not discounting plasmid's analysis (since I do not know the answer to this one), one point what you said above seems wrong to me:
The "expected value" or mean does not assume uniform probability distribution.
The equation,
mean = 1/n * (sum of all samples)
works for any distribution.
(Actually, we can calculating the expected value of the mean above, since the mean can only be calculated if the exact probability distribution is known up-front).
And indeed, even if the machine may be programmed to never produce a 5, the expected value can be 5.
-
I would agree with gavinksong that...
...the best way to bet with Bob would be to guess the mode, which with the number distribution that was shown would be 9.
For Alice, you would have to look at the actual distribution and, for each number, count out how many times you see a number appear within any given margin.
The distribution is:
1: 3
2: 1
3: 2
4: 2
5: 0
6: 3
7: 0
8: 1
9: 5
The optimal guesses if you knew the error margin would be
Error margin 1: either 8 or 2 (both had 6 hits within +/- 1)
Error margin 2: either 7 or 8 (9 hits within +/- 2)
Error margin 3: 6 (13 hits)
Error margin 4 or greater: 5 (everything)
If you have absolutely no idea what Alice's error margin is, then you can't give a definite answer. If you know the error margin is likely to be either 1 or 2, then go with 8.
Thanks, this is interesting

I agree with you on the answer to be given to Bob. This would be 9.
I understand your approach.
But the integer closest to mean (or the "expected" value) turns out to be 5, which the last choice in your argument.
(Actually, I constructed the list of samples with the intent of keeping the expected value to be exactly 5, with the number of samples as 18, totaling to 90. But I see now that I made some mistake and hence the number of samples have become 17, yielding expected value as ~ 5.3. Fortunately, doesn't affect the results drastically - the closest integer is still 5 at least).
The S.D for the samples turns out to be ~ 3.1378, yielding SEM to be: 3.1378/sqrt(17) = 0.761.
Question is: Should mean be used or should Charlie go with your analysis..?
-
@k-man and @DejMar: you have poked a few holes into my question

Let me clarify:
a. The numbers a1, a2, ..an and x, y can have duplicates. Each number is picked using a function like, rand(1, S), which gives a random integer in the specified range.
b. S is always even (this is the easiest way to escape the mid-point issue pointed out in your post). The first question is now modified as: "A. Guess whether the number I'm going to tell you now is (less than or equal to S/2) or (more than S/2)". I think S = 2 case must be allowed as well.Would your responses change then?
@k-man, thanks for the wikipedia link - was interesting to read. It doesn't apply here (at least not directly) because we can have repeats - as you have pointed out yourself. -
For (A), one approach would be to estimate S, based on a1 to an.
-
Is there any sort of probability distribution for Alice's margin of error? Can it be anything between 0 and infinity?
Let's see if there are any other thoughtsI would just guess whatever is closest to the mean value for Alice, and the mode for Charlie.

No.. nothing of that sort.. It is non-zero, most likely just "1", or at the max "2", if she is feeling generous.
Also, to clarify, your answer is the same as what I thought was right.
-
Is there any sort of probability distribution for Alice's margin of error? Can it be anything between 0 and infinity?
Let's see if there are any other thoughtsI would just guess whatever is closest to the mean value for Alice, and the mode for Charlie.

No.. nothing of that sort.. It is non-zero, most likely just "1", or at the max "2", if she is feeling generous.
-
There's no need to have Bayes meddling with this problem.
If you have a coin with probability p of landing heads, then the probability of tossing H heads out of N tosses is
f(p) = pH * (1-p)N-H * (N choose H)
which is a polynomial in p. Since we're dealing specifically with the case of N=10 and H=5, we have
f(p) = p5 * (1-p)5 * 252
f(p) = 252 * (p5 - 5*p6 + 10*p7 - 10*p8 + 5*p9 - p10)
That function f(p) describes the probability that tossing a p coin 10 times will yield 5 heads. If we're given the fact that 5 heads were tossed out of 10 and we're asked to calculate the probability that p is within a range, then we can integrate f(p) and compare the value within that range to the total integral from 0 to 1.
Integral[f(p)] = 252 * (1/6 * p6 - 5/7 * p7 + 10/8 * p8 - 10/9 * p9 + 5/10 * p10 - 1/11 p11)
The integral from 0.45 to 0.55 is
Integral[f(p)](0.55) - Integral[f(p)](0.45)
= 252 * (0.00461344 - 0.01087454 + 0.01046674 - 0.00511707 + 0.00126648 - 0.00012665)
- 252 * (0.00138396 - 0.00266907 + 0.00210189 - 0.00084076 + 0.00017025 - 0.00001393)
= 0.0575568 - 0.03334968
= 0.02420712
The integral from 0 to 1 is
252 * (1/6 - 5/7 + 10/8 - 10/9 + 5/10 - 1/11)
= 0.09090909
So the probability that p is between 0.45 and 0.55 is approximately
0.02420712 / 0.09090909
= 0.26627832
Well, I suppose you could say that it implicitly relies on Bayesian analysis in a way that I just don't draw attention to in this approach.
My method is exactly the same. Both you and gavinksong came to the same conclusion, within few mins of each other.
..The best estimate for p has probability 0 of occurring. Of course, this is not surprising or counter-intuitive. The best estimate for p is one that has the least error..
@plasmid, it is Bayes' rule indirectly

Let,
A be the outcome that "p is between r and r+dr (where dr is an infinitesimally small increment of r and 0 < r < 1)".
B be the outcome that "5 heads turn up in 10 coin tosses".
Then the a priori probability p(A) (probability of A, given no other data) is nothing but 'dr'. Let a priori probability of B be p(B). This is the probability that B will occur ("5 heads turn up") , when we do not know what is p (the probability of heads). We may not know what is p(B), but we can readily agree that p(B) will not depend on r.
We also have,
p(B|A) = Probability of B occurring, given that A has occurred = 10C5.r5.(1-r)5
By Bayes theorem,
p(A|B) = Probability of A occurring, given that B has occurred
= p(B|A). p(A)/p(B)
= 10C5.r5.(1-r)5.dr/p(B)
Now, if we integrate p(A|B) over the interval (0, 1), we must get "1" - i.e, it is a certainty that r is in the range (0, 1). Using this, we can calculate p(B) = Integral[10C5.r5.(1-r)5.dr] over r = 0..1.
Plugging this back in the equation above, and again integrating over the interval [0.45, 0.55], we get the desired answer, which both plasmid and gavinksong have provided already.
Now, why I described all this is, I found how p(B) becomes Integral[10C5.r5.(1-r)5.dr] over r = 0..1 to be interesting!
It is like, I have this question - what is the chance of rain for next five days, if you do not know what is the "probability that it will rain on any given day"? The question seems slightly absurd, but has a perfectly valid expression.
Of course, if we think about the question again, we arrive at the same result directly.. But, I just found it to be interesting

The 44th Riddle
in New Logic/Math Puzzles
Posted
Question: what happens when there are only 2 bankers left?
Say the elder one suggests an allocation. If the younger one rejects - who gets all the ingots?