
bubbled
-
Posts
93 -
Joined
-
Last visited
-
Days Won
2
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by bubbled
-
-
Is it OK assume exactly 4 busses per hour, but arriving at completely random times? I can simulate that. Clearly, if the city had the busses arrive at exactly 15 minute intervals, then wait times would average around 7.5 minutes. And no one would ever wait longer than 15 minutes.
-
I think I figured out the first question:
SpoilerDefine N (even number) to be the number of chips in the pot. As long as N is not equal to a number 2^n (n = integer), then Turkey (T) should go first. Otherwise go second. If N is odd, the game is trivial. T takes 1 on the first move and wins.
If N is not equal to 2^n, then search for the smallest number 2^a where (N / 2^a) is an odd number. Start by taking 2^a from N. If the homunculus (H), takes an odd number next, the game is over. T takes 1 next and will win. So, to keep things interesting, H must take an even number next.
(N - 2^a) will be divisible by all numbers 2^b where b <= a. And (N - 2^a) / 2^b will be an even number. Therefore, if H takes 2^b next, (N - 2^a - 2^b) will be divisible by 2^b and will be odd. So, whatever even number, 2^b, H takes from (N - 2^a), T should next just take 2^b. H can now take 2^c where c <= b, and T continues with the same strategy above until he wins.
If N = 2^n, then N / 2^a (a <= n) will be even. So no matter what even number H takes from N, T can go second and take 2^a next, and continue the strategy above to win.
In the specific game with 43546758343209876 chips in the pot, T should go first and take 4. 43546758343209876 - 4 = 43546758343209872. That number is divisible by 2 and 4, and those divisions result in an even number. So, no matter whether H takes 4 or 2 next, he will leave an odd number of 4's or 2's for T.
Here's one concrete example. If N is 20:
T takes 4, H 4, T 4, H 4, and T wins with 4. Or T takes 4, H 4, T 4, H 2, T 2, H 2, T wins with 2. Or T takes 4, H 2, T 2, H 2, T 2, H 2, T 2, H 2, T wins with 2.
-
There are twenty-four half-dollar coins stacked in three identical piles. Two piles are real and one is counterfeit. The individual counterfeit coins look exactly like the others but either weigh a gram more or less from the others. The net weight of each pile is exactly the same. How many weighs on a balance will it take to determine which pile is false?
How many weighs would it take if there were an equal distribution of false coins in each pile?
Agree with Ed on first part. Can you clarify the second question?
-
Here are my results:
Hidden Content
Hmm:
I didn't find A > B, I just found A >= B.
Here are my results:
Hidden Content
Hmm:
Hidden Content
Re-ran the script with a couple of changes:
A > B zero times. And A = B 11 times.
-
Here are my results:
I ran 10,000,000 simulations and found A > B 12 times. It's very very rare.
Here's my 10 lines of code. This problem is made for Python/numpy.
import numpy as np
import numpy.matlibdef A_or_B():
kids = np.matlib.rand(10, 20)
return np.amax(np.amin(kids, axis=0)) < np.amin(np.amax(kids, axis=1))
oddball = 0
for i in range(10000000):
if not A_or_B():
oddball += 1
print oddball -
I just ran one more 100M simulation and captured a lot more info.
Probability that a new random point will fall in the largest arc: 0.61104318
Mean of the arc length that captures the random point: 0.499978733972
Mean of the sums of the squared arc lengths: 0.500018084204
Median length of the longest arc: 0.591768881555
Histogram of the shortest arc lengths:
Histogram of the middle arc lengths:
Histogram of the longest arc lengths:
I might be the only one, but I find these graphs to be interesting. Anytime you have two or more random variables and are trying to say things about their relationships to each other, things get pretty non-intuitive.
-
@bubbled, our numbers agree, including sum of the squares of means being 0.426...
I also find that the mean of the sum of the squares is 0.500.
I think it's interesting that the sum of the squares of the means doesn't match the mean of the sum of the squares.
Maybe that shouldn't be interesting?
-
I ran a simulation of 100,000,000 trials using bonanova's method (I think) on a unit circumference. I pick two random numbers, P1 and P2, between 0 and 1.
If P1 < P2, then my three lengths are L1 = P1, L2 = P2 - P1, and L3 = 1 - P2.
If P2 < P1, L1 = P2, L2 = P1 - P2, and L3 = 1 - P1.
I sort the three lengths and put them into a matrix where the first column consists of all the shortest lengths, the second column is the middle length and the third column is the longest length. I then calculate the mean of the various columns.
I get this result:
mean of longest arcs = 0.611101750112
mean of middle arcs = 0.277769774084
mean of shortest arcs = 0.111128475804
This matches bonanova's results pretty closely and those lengths add up to 1, as expected.
It would seem to me that the probability that a particular point falls in the longest arc should be 0.6111...
And the middle arc 0.277... and shortest arc 0111...
Which means that the average length of the arc that a random point (or fixed point) falls in should be the sum of the squares of the mean arc lengths. However, the sum of the squares is only 0.462950934519. I would expect it to be .5, given the analysis from the previous problem.
I'm a bit confused. Thoughts?
OK, so I continued by using bonanova's idea of picking the arcs and then spinning the wheel. I used the same method as above (picking two random points) and creating three arcs. I then pick a random new point and find the length of the arc it falls in. I store those lengths in a separate array and find the mean length.
With 100,000,000 million trials, I get 0.500034371498. This it what we'd expect. But I'm confused as to why the sum of the squares doesn't add up to .5 as well.
It must be something to do with the distribution of the actual lengths of the arcs. Maybe because when the longest arc is bigger than the mean of the other longest arcs, the random point will fall in it more often? More simulations necessary to answer that question.
-
I ran a simulation of 100,000,000 trials using bonanova's method (I think) on a unit circumference. I pick two random numbers, P1 and P2, between 0 and 1.
If P1 < P2, then my three lengths are L1 = P1, L2 = P2 - P1, and L3 = 1 - P2.
If P2 < P1, L1 = P2, L2 = P1 - P2, and L3 = 1 - P1.
I sort the three lengths and put them into a matrix where the first column consists of all the shortest lengths, the second column is the middle length and the third column is the longest length. I then calculate the mean of the various columns.
I get this result:
mean of longest arcs = 0.611101750112
mean of middle arcs = 0.277769774084
mean of shortest arcs = 0.111128475804
This matches bonanova's results pretty closely and those lengths add up to 1, as expected.
It would seem to me that the probability that a particular point falls in the longest arc should be 0.6111...
And the middle arc 0.277... and shortest arc 0111...
Which means that the average length of the arc that a random point (or fixed point) falls in should be the sum of the squares of the mean arc lengths. However, the sum of the squares is only 0.462950934519. I would expect it to be .5, given the analysis from the previous problem.
I'm a bit confused. Thoughts?
-
Hidden Content
Hidden Content
Hidden Content
Hidden Content
Expanding on my post of Sunday at 8:09 AM:
Hidden Content
I can't disagree with any of this. I was completely wrong and the fact that my answer matched with the correct answer blinded me to the fact that I was introducing an extra point into the problem. I now realize that you have to be very careful with how exactly you apply random conditions to problems like these.
-
Hidden Content
The more I've thought about my solution, the more I think it does apply to OP.
I really like your approach too, but I don't think it's a coincidence my solution also arrived at half the total arc. Since the three cuts are randomly chosen, it doesn't matter whether we pick a fixed point and then pick three cuts, or if we pick the random cuts first, and then pick a random point. Either way, once we have the fixed point and the three cuts, we can unroll the arc and do the calculation I suggest.
IMO, the OP cleverly disguises that, indeed, there ARE 4 random arcs and on average they are 25% each. And the fixed point to one random point and the fixed point to another of the random points will capture 50%.
I like your idea of spinning the circle with three cuts and realizing that the largest cut, on average, figures to contain the point in question. But seeing that the fixed point carries the same weight as the three cuts, has value as well. Sometimes, there are many ways to skin a cat. I'm sure your solution generalizes better and might be "safer" here, but I think I got it as well.
-
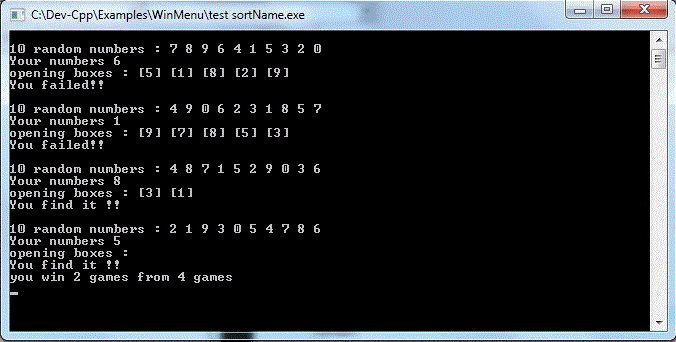
I think bubbled is right,
"Sorting like" strategy, without "real sorting" will not work.I have proposed this "Sorting like" strategy, exactly like plasmid.
How about this :
Hidden Content
but then I realize it was not working. I've tested it using dev-C++.
the chance to find your name is only 50%, the same chance with random way opening boxes.in my program : box numbered from 0 to 9, and your number is random from 0 to 9. You can only open 5 boxes to find your name.
Yes, it does work:
jasen , you were the first in this thread to suggest the right answer. But, because it involved moving the boxes (forbidden) and then you lost faith, bonanova correctly didn't mark it as solved. I recall many years ago, encountering this problem and having the "ah ha" moment where I thought of the solution and was "certain" it must be correct. However, I probably spent another 6 hours just thinking about why (I couldn't code then).
The point I was making earlier about never doing better than 50% still stands. This strategy creates correlated results more powerfully than any other guessing puzzle I've seen. As soon as 1 or 2 prisoners are successful, the chances the next prisoner succeeds starts to trend towards 100%. In fact, if the first prisoner were to not find his name until the 50th box, the next 99 prisoners would be guaranteed to win!
For the purposes of discussion, lets assume that every prisoner will keep looking until he finds his name (using the strategy plasmid suggests). Yes, if a single prisoner fails to find their name in 50 boxes, they all lose. But for science, they will all go into the yard and look into the boxes.
If a prisoner fails to find his name until 80 boxes, the rest of the prisoners have their fate already set in stone. Exactly 79 other prisoners will take 80 boxes to find their name (lose together), and 20 will all find their name in <= 20 boxes.
As I said, their is no way to improve the odds of a single prisoner finding his name, but the strategy will create a result space where a single success breeds massive correlated success and a single failure breeds massive correlated failure. Which is cool.
-
At a track meet, you have 25 runners for a 100 meter event and only 5 lanes. You've forgotten all of your timing devices at home. Assume that all runners {R1, R2,...R25} run the event in different times from each other, but an individual runner RN, will run the event in the same time each time he/she runs.
Your job is to figure out who is the 1st, 2nd and 3rd fastest runners. What is the minimum number of heats needed to make your determination?
-
Here's another try at distinguishing our ways of looking at this problem.
Hidden Content
I was close to answering, but didn't understand my result yet:
I picked three random numbers between 0, 1. I then sorted them from smallest to largest and calculated (1 - largest + smallest). On average, I was getting .5. Translating that to picking three random points between 0, 2pi would thus arrive at pi as the average length of the arc you are looking for. I guess the easiest way to look at it is if you were to pick three random numbers between 0, 2pi on a number line (not a circle), those three numbers would create four sections, and each section would average pi / 2. By picking a point, any point, you are essentially getting two of those sections, on average.
Still don't feel like I totally "get" it.
-
OK, and I have a suspicion that my answer is too easy and there's more to it.
Nope:
Hidden Content
my suspicion is that given that most people would pick a particular round to use their ability that there is in fact a particular advantage even if the expected payouts are the same. Maybe game theory should be utilized here over strict statistics??
This feels very subjective. I simulated the event using the three different options 1M times each. Here's what I get with graphs. Seems like it totally depends on your appetite for risk:
Hidden Content
One follow-up:
Hidden Content
would this not imply that the first two rounds use for the magic power are worst. Imagine that you are trying to beat your best score, your opponent is yourself. An opponent with the exact same power. Trying to do the best in this case, according to your previous post would include using this power at the end. Hence there is an advantage.
OK, I agree, but it's really really thin. First of all, I might be a cowboy and want to maximize my chances of turning 8 into 128. In that case, I'd use the power on first two rounds. And who's to say that's wrong? if you put clear parameters in place, like "minimize chance of ruin," I'm totally with you.
Also, if you offered me $.50 to use my power first two rounds, I'd be foolish not to.
In the case where we are taking about $8 at risk, you can't make a definitive choice and say it's "right." If we say a player has to risk all the money they have in the world, now I'm feeling like it's clear that last two is right.
-
OK, and I have a suspicion that my answer is too easy and there's more to it.
Nope:
Hidden Content
my suspicion is that given that most people would pick a particular round to use their ability that there is in fact a particular advantage even if the expected payouts are the same. Maybe game theory should be utilized here over strict statistics??
This feels very subjective. I simulated the event using the three different options 1M times each. Here's what I get with graphs. Seems like it totally depends on your appetite for risk:
Hidden Content
One follow-up:
The only way I could imagine using game theory or human psychology to decide, is if my goal was to beat a theoretical opponent who is granted the same ability. In that case, I maximize my chances of "beating" him by using my ability on the last two rounds. If he chooses the same thing, we have an equal chance of beating each other. But, if he chooses either of the other two options, I am more likely than not to finish ahead of him.
-
OK, and I have a suspicion that my answer is too easy and there's more to it.
Nope:
Hidden Content
my suspicion is that given that most people would pick a particular round to use their ability that there is in fact a particular advantage even if the expected payouts are the same. Maybe game theory should be utilized here over strict statistics??
This feels very subjective. I simulated the event using the three different options 1M times each. Here's what I get with graphs. Seems like it totally depends on your appetite for risk:
16 teams, $8 starting bankroll.
Magic power last two rounds (my choice): mean 32.006668
My choice has nothing to do with the fact that the mean happened to be a tiny bit better. Instead, I would always choose the strategy that reduces the chance of ruin by 7-1 (versus middle two) and 9-1 (versus first two).
Magic power middle two rounds: mean 31.980512
Magic power first two rounds: mean 31.993984
-
OK, and I have a suspicion that my answer is too easy and there's more to it.
Nope:
I think you were right. It doesn't matter how many rounds there are. Your total EV will never change on the rounds where you have to guess. So your finishing money will always be S * (2^R) where S = starting money and R = number of rounds you can know the results.
Let's say you start with $8, in this 16 team tournament and your magical power is during...
first two rounds: 8 (start) -> 16 (after round 1) -> 32 -> 32 -> 32
middle two rounds: 8 -> 8 -> 16 - > 32 - > 32
last two rounds: 8 -> 8 -> 8-> 16 -> 32
However, I would definitely use the power on the last two rounds to minimize chances of ruin.
-
Not solved yet.
Here goes:
I'd go up 2-love in sets, tied 6-6 in games and up 6-0 in the tiebreaker. At the end of the day, the set score is meaningless. And I'm betting on Djoker against any true amateur.
-
@bubbled, I would interpret it this way:
Round 1: Four games => 4 winners.
Round 2: Two games => 2 winners.
Round 3: One game => 1 winner.Seven games in all, and there are no "middle two" rounds.
If that's right, my take is
Hidden Content
I agree. But
I would use my power on the last two rounds as that will make my probability of losing it all 1/16. Same expected profit, $12, but less volatility.
-
A few clarifications. It seems like you are expecting there to be 4 rounds? In that case, there needs to be 16 teams. I'm also assuming that each game is 50-50 and you have no insight into the outcome?
-
Here are three nudges. Not exactly clues. More like clarification of various points covered in the OP
Hidden Content
Hidden Content
Hidden Content
And here is a slight "Oops."

Did I forget to mention that the boxes are externally numbered 1-100?
They are, and now the OP says so.bonanova I strongly disagree:
The statement, "...and gives each of them an expectation of finding his name that is significantly greater than 50%." is (and must be) incorrect.
Whenever you have a guessing game that entails a group strategy, there is no way to improve the chances of an individual succeeding in the guessing game, whether it be red and blue hats, or boxes with names in them. If I'm one of the prisoners, I will be exactly 50% to find my name in the 50 boxes I look in, no matter what strategy I use.
However, the strategies in these games cleverly manage to cluster the wins and losses to increase the group's chances of being successful. In this case, that strategy has an enormous effect. But, if we were to run this game 1000's of times, including making all 100 prisoners complete the game even when one of the earlier prisoners failed, you'd find that exactly 50% of the prisoners would be successful. Clearly, if you are prisoner #80, and no one has failed ahead of you, you are very likely to succeed using the proper strategy. However, if you knew a prisoner had failed ahead of you, you might be very unlikely to succeed. This is the only way the miraculous 30+% success rate is possible.
Given the tremendous solving skills you've demonstrated over the years, I imagine you already know this and was just a little sloppy in the above statement. I just didn't want anyone to be lead astray.
There is no way to improve the inherent odds of a guessing game, and remembering that will usually lead you in the right direction for these group puzzles.
-
I'll go for it again:
My answer is C
Going left to right and up to down. I see one line disappear. The remaining line stays in place as the line that disappeared reappears two clicks clockwise. Then the line that stayed in place, disappears, and then reappears two clicks clockwise. C fits that pattern.
-
 1
1
-
-
Hidden Content
We done bonanova. Here's a link to his wiki page that mentions that bet: https://en.wikipedia.org/wiki/Titanic_Thompson
Here's a good biography about him. Interesting life: http://www.amazon.com/Unsinkable-Titanic-Thompson-Carlton-Stowers/dp/0963401580
He certainly personifies my favorite line from Guys and Dolls:
One of these days in your travels, a guy is going to show you a brand-new deck of cards on which the seal is not yet broken. Then this guy is going to offer to bet you that he can make the jack of spades jump out of this brand-new deck of cards and squirt cider in your ear. But, son, do not accept this bet, because as sure as you stand there, you're going to wind up with an ear full of cider.

Take the last chip
in New Logic/Math Puzzles
Posted
I think have the answer to the second part:
Turkey (T) should go first unless the starting chips are in the set of losing (L) starting conditions.
L = {L1 = 2, L2 = 3, L3 = L1 + L2, L4 = L2 + L3, L5 = L3 + L4....}. So it's the Fibonacci sequence without the 1, 1 at the start as those numbers don't make sense given the problem.
My logic is a bit convoluted, but it's the only way I've managed to get anywhere. Basically, the key numbers are the ones in L. There are two ways to win.
1. Ideally, on your first play, take as many chips as necessary to leave a number in L. However, you can only do this if the number of chips you take is strictly less than 1/2 of the number of chips you leave. For example, if your starting chips is 7, you can take 2, and leave the homunculus (H) with 5, and since 2 < (5/2) and 5 is in L, you win. However, you lose on 8, because if you take 3 leaving 5, H can win by taking the rest of the chips. So you must take either 1 or 2, but either way, H will leave you with 5 next, and you lose.
2. You also win if the (starting chips) - (the largest member of L that's less than starting chips) is not in L. For example, let's look at 20 chips to start. The key number is 13, as that's highest number in L that is less than 20. Ideally, we'd like to get right down to 13, but if we take 7, H wins by taking the rest of the chips. But, we are in luck as 20 - 13 = 7, and 7 in not in L. This means we can play the game as though the starting chips were 7. Once we take the last chip above 13, we will leave H with 13 and win.
If the number of starting chips gets really large as in the problem, the only way I can think solving it is recursively. The idea is, you need to keep leaving H with various numbers in L, all the way down the ladder. To do that, you may need to examine how you win from smaller numbers and build up. In example 2 above, I know that 7 is a winner. I also know that 5 is a loser, so I'd take 2, leaving 18 which is 5 more than 13. H can take any number from 1-4, but none of those will get him to 13. The most interesting is 1, leaving T with 17. 17 is 4 more than 13, so all still good. We know 3 is in L, so T takes 1, leaving H with 16, which is 3 more than 13. H can take 1 or 2, but either way, T's next play will leave H with 13. Next, T just needs get to the next stop which is 8. He will repeat the above process, stopping at 11 and/or 10 to get there. Then he'll go from 8 to 5, 5 to 3, and then win.