-
Posts
142 -
Joined
-
Last visited
-
Days Won
1
Content Type
Profiles
Forums
Events
Gallery
Blogs
Posts posted by mmiguel
-
-
Spoiler
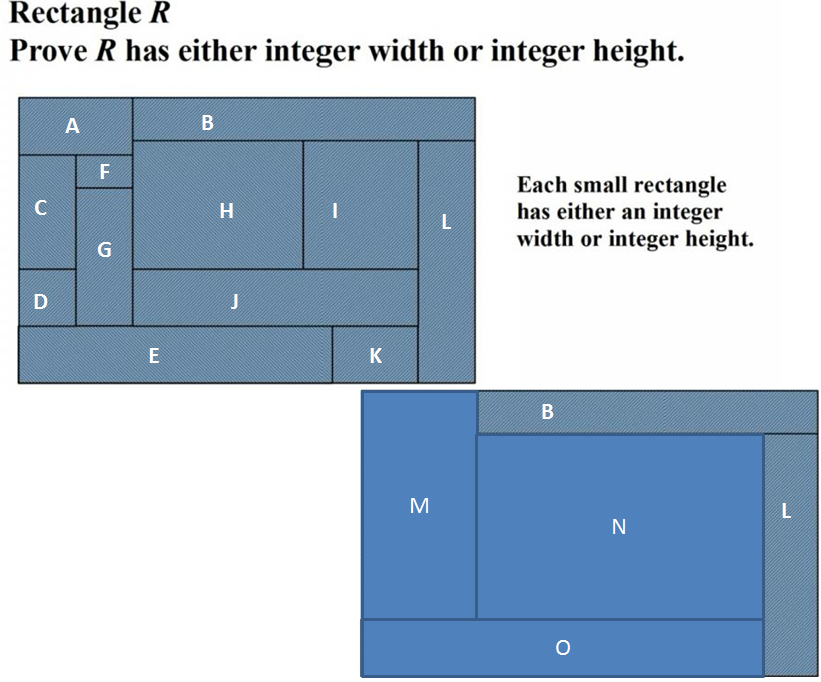
Consider this simpler sub-problem.
Two boxes, X and Y, share a side. Another box, Z is congruent to the union of X and Y.
Figure 1below shows that if X and Y have integer width or height, then so must Z.
<SEE FIGURE 1>
Furthermore we can replace X and Y by Z and still maintain the problem assumptions, but simplify the problem.
By applying this concept multiple times, one can construct the simplified problem in figure 2.
<SEE FIGURE 2>
First merge C and D; then merge F and G; then merge the results of the last two merges; Then merge that third result with A to get M.
Merge H and I; then merge that with J to get N
Merge E and K to get O
So now we have the simpler problem with B,M,N,L, and O.
B (like any other rectangle,) can have either integer width or height, so let's divide our analysis into these two cases. Under those two cases we must show that we cannot assign selections of integer width/height to the other rectangles such that the entire rectangle has neither integer width nor integer height.
IF B has integer width instead of height:
- To prevent the whole rectangle from having integer width, M must have integer height instead of width. But this means that O must have integer width instead of height; and this means that L must have integer height instead of width.
- We get to the case in Figure 3
- <SEE FIGURE 3>
-
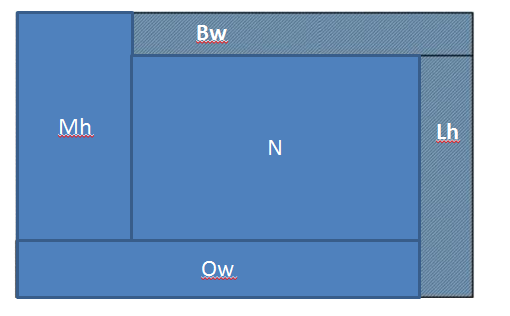
- If N has integer width, then so does the whole rectangle because of B and O
- If N has integer height, then so does the whole rectangle because of M and L
- So if B has integer width (our antecedent), then the whole rectangle is guaranteed to have integer width or height
Alternatively, IF B has integer height instead of width:
- To prevent the whole rectangle from trivially having integer width/height, we must choose L to have integer width instead of height; This leads to assigning O to have integer height instead of width; This leads to assigning M to have integer width instead of height.
- We get to the case in Figure 4.
- <SEE FIGURE 4>
-
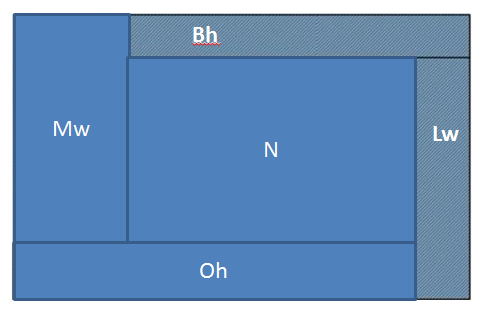
- If N has integer width, then so does the whole rectangle because of M and L
- If N has integer height, then so does the whole rectangle because of B and O
- So if B has integer height (our antecedent), then the whole rectangle is guaranteed to have integer width or height
Combining the two cases above, regardless of whether B has integer width or height, the whole rectangle is guaranteed to have integer width or height.
-
 1
1
-
Spoiler
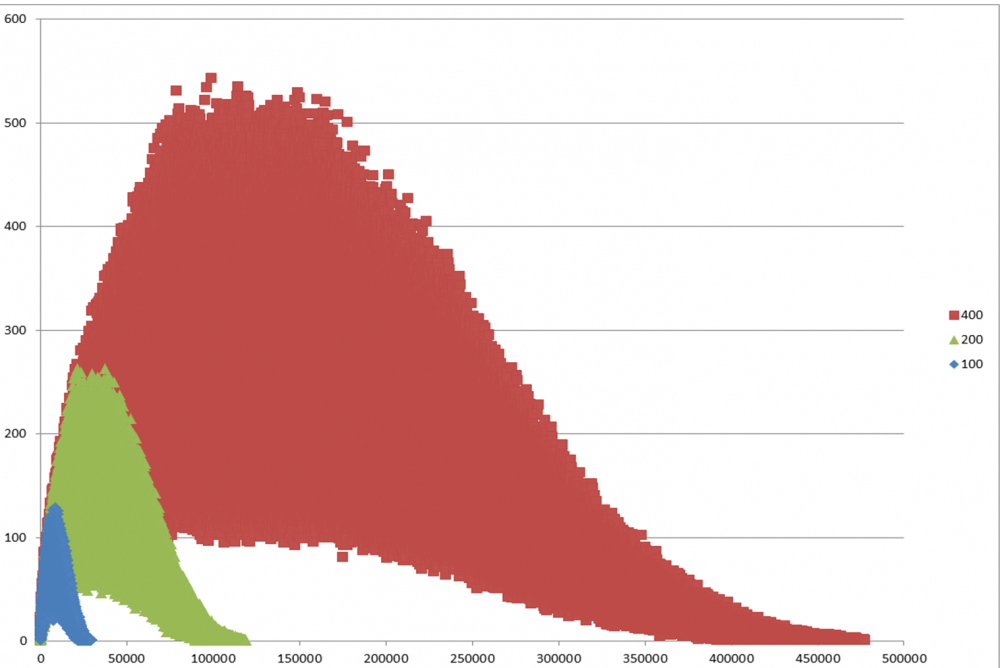
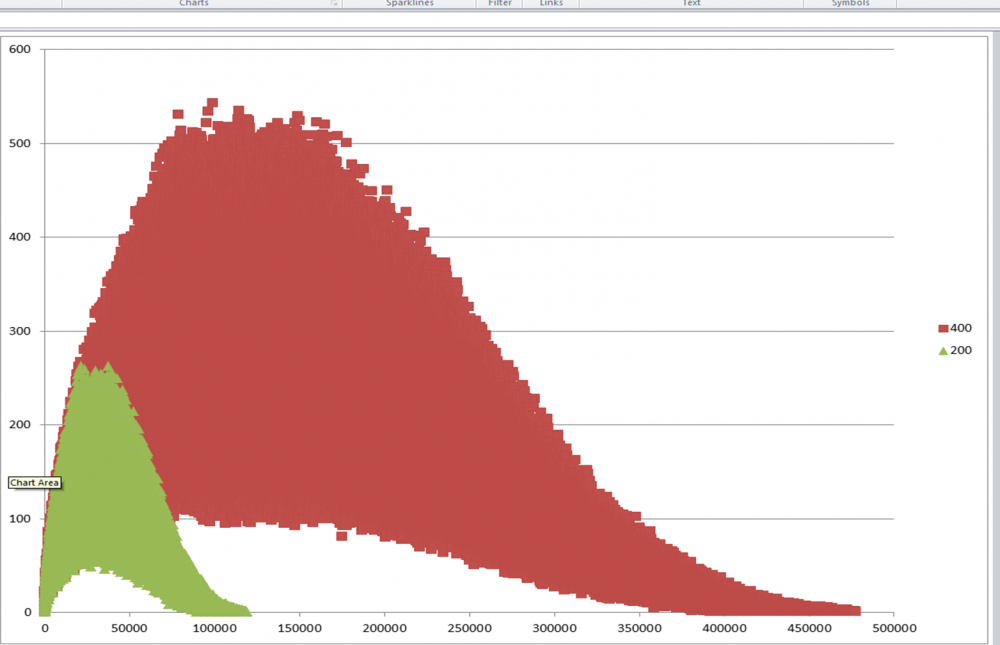
I believe you can represent any positive integer as at least one of t(a) + S(b) + P(c) (allowing a, b, or c to be zero)
I wrote a script to sweep a,b, and c from 0 to some target value each, and record the resulting integers.
For each resulting integer, we count the number of (a,b,c) representations associated with that value.
As long as the number of representations is non-zero for all positive integers, then every integer is expressible by this form.
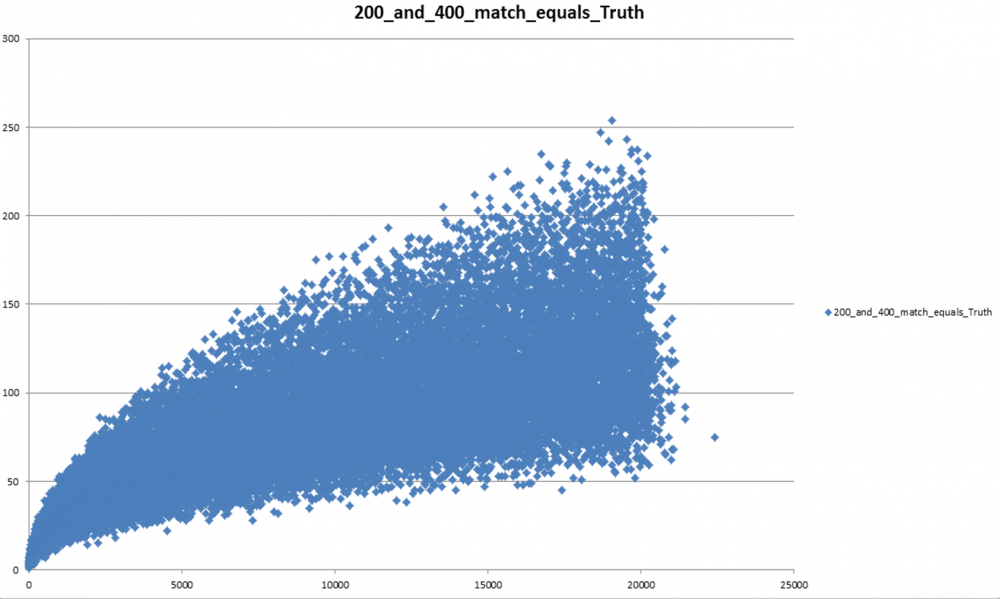
I plotted the number of representations as a function of resulting integer for sweep targets of 100, 200, and 400.
The third plot is the set of points where the 200 run matches the 400 run, which should be truth (i.e. the same as if we went to infinity).
The max and min envelope of this "truth" plot look roughly logarithmic. I would be very surprised if any positive integer drops to zero.
Therefore I think all positive integers have at least one representation and your conjecture is correct.
Spoilerdef fa(a):
return int(0.5*a*(a+1));
def fb(b):
return int(b**2);
def fc(c):
return int(0.5*c*(3*c-1));
def f(a,b,c):
return fa(a) + fb(b) + fc(c);target = 100;
seen = {};
for a in range(target):
for b in range(target):
for c in range(target):
z = f(a,b,c);
if not z in seen:
#seen[z] = []
seen[z] = 0;
#seen[z].append((a,b,c))
seen[z] += 1;
#seen = list(sorted(seen));
for i in range(int(max(seen))):
if not i in seen:
print i;
break;
out = [];
for z in sorted(seen):
out.append((z,seen[z]))
with open('out_%d.csv' % target,'wb') as f:
f.write('\r\n'.join('%d,%d' % r for r in out)); -
Spoiler
a = pi
c = a^b = 2
b = ln(2)/ln(pi)
-
Spoiler
7ft
-
Answer for n = 2e9
Spoiler407
Took too long to run in python, so rewrote in C.
#include <stdio.h>
#include <math.h>int main(void){
unsigned int a,b,c,i,n;
n = 2*pow(10,9);
if (n == 1){
printf("%d",5);
return 0;
}
if (n == 2){
printf("%d",27);
return 0;
}
i = 2;
a=5;
b=27;
while (i < n){
c = (6*b-4*a+1) % 1000;
a = b;
b = c;
i++;
}
printf ("%d",b % 1000);
return 0;
} -
Rationale
SpoilerLet r5 = sqrt(5)
Let a=3+r5
Problem is find f(n) = last 3 digits before decimal point of a^n
Let a' = 3-r5 (the conjugate of a)
Note that a*a' = 4 and a + a' = 6
As DeeGee showed, a^2 = (3+r5)^2 = 9+6r5+5=14+6r5=14+6(a-3)=6a-4
So a^2 = 6a-4
Therefore a^n = 6a^(n-1) - 4a^(n-2)
Similarly for a': a'^2 = (3-r5)^2 = 9-6r5+5=14-6r5 = 14+6(a'-3) = 6a'-4
So a'^2=6a'-4
Therefore a'^n=6a'^(n-1)-4'^(n-2)
As a first try, consider g(n) = a^n + a'^n
Since a' < 1, then a'^n for all n is also < 1.
So a^n = g(n) - a'^n and the last 3 digits of a^n will be the last 3 digits of g(n)-1
g(n) = a^n + a'^n = (6a^(n-1) - 4a^(n-2)) + (6a'^(n-1)-4'^(n-2)) = 6*(a^(n-1) +a'^(n-1)) - 4(a^(n-2) +a'^(n-2))
g(n) = 6*g(n-1) - 4*g(n-2)
As a second try, consider h(n) = g(n) - 1 = 6*(h(n-1)+1) - 4*(h(n-2)+1) - 1 = 6*h(n-1)-4*h(n-2)+6-4-1 = 6*h(n-1)-4*h(n-2)+1
h(n) = 6*h(n-1)-4*h(n-2)+1
This is a recursive solution of degree 2, so we need two initial conditions.
g(1) = a + a' = 6, so h(1) = 5
g(2) = a^2 + a'^2 = 28, so h(2) = 27
So these three things define a recursive algorithm to get h(n):
1. h(1) = 5
2. h(2) = 27
3. h(n) = 6*h(n-1) - 4*h(n-2) + 1
We will still run out of memory, so we need to throw away things that don't matter.
Consider h(n) = x(n) + y(n) where y(n) = h(n) % 1000 (i.e. modulo 1000) and x(n) = h(n) - y(n)
x(n) cannot impact y(m) where m > n. This is because the future impact of x(n) is 6*x(n), followed by a -4*x(n).
So the two components of the future sum due to x(n) is first 6*x(n), followed by 2*x(n) because 2 = 6-4.
Neither of those components have any residual modulo 1000.
Therefore we can define f(n) = h(n) % 1000.
The final definition is:
1. f(1) = 5
2. f(2) = 27
3. f(n) = 6*f(n-1) - 4*f(n-2) + 1 % 1000
-
Spoiler
Python answer
def sol(n):
if n == 1:
return 5;
if n == 2:
return 27;
a=5;b=27;i=2;
while i < n:
c = 6*b-4*a+1 % 1000;
a,b = b,c;
i += 1;
return b % 1000;I think I got the answer thanks to some of the other hints and ideas posted.
-
also... my denominator's are ordered (i.e. left, up is different than up left), but the pile analogy is not - both cases are (1,1).
doh!
-
i never imposed the limit that you can have at most n stones in a pile....
so it's not purely an unlimited number of binary decisions...
won't worry about fixing it now... off to sleep
-
i probably oversimplified this and don't have the right answer for the 3x case, but oh well - i'm tired
same idea, except that George has three times as many stones as Lennie.
It is still true that collisions occur only with 2*n stones, but now, George has 3/4*2*n= 3n/2 stones, whereas Lennie only has n/2 stones.
If n is odd, then there won't be any state with 2*n stones (assuming both make their move simultaneously, before we say the next state has begun).
For example, if n is 3, then there won't be a case where there are a total of 6 stones:
(G,L) will evolve like (3,1)=4stones, then (6,2)=8 stones, etc
If n is 4, though, we saw in the last example that we do reach 2*4=8 stones.
So if n is odd, the probability of collisions becomes zero... assuming collisions occur when they are sitting on the same spot in the same state, and not while transitioning between states...
The enumeration of collisions is:
(n/2,n,n/2,0)
(n/2+1,n-1,n/2-1,1)
...
(n-1,n/2+1,1,n/2-1)
(n,n/2,0,n/2)
Thus there are (n-n/2+1) = n/2+1 collision states (indexing off the first number).
Assuming George's three moves do not have to all be in the same direction, George has 3*n/2 independent binary decisions, whereas Lennie has n/2 independent binary decisions.
Thus the answer (given the assumptions above) is:
(n/2+1)/(2^(3n/2)*2^(n/2)) = (n/2+1)/(2^(2n))
The denominator is the same as before, but the numerator changes from n+1 to n/2+1
0 : 1.01 : 0.3752 : 0.1253 : 0.03906254 : 0.011718755 : 0.003417968756 : 0.00097656257 : 0.0002746582031258 : 7.62939453125e-059 : 2.09808349609e-0510 : 5.72204589844e-0611 : 1.54972076416e-0612 : 4.17232513428e-0713 : 1.11758708954e-0714 : 2.98023223877e-0815 : 7.91624188423e-0916 : 2.09547579288e-0917 : 5.52972778678e-1018 : 1.45519152284e-1019 : 3.81987774745e-1120 : 1.00044417195e-11If transitioning results in an allowable collision, then let n be odd, and just plug it into the formula (like above).
-
At each move, each player has two choices (George can go up or can go right, Lennie can go down or can go left).
Consider an alternative formulation where each player has two spots, and they may choose to pile a rock in either spot to form two piles.
Each player has 2*N rocks, and a pile can only be N high.
What is the probability that George's pile is the (n-minus) mirror of Lennies?
i.e. if Lennie has one pile with x stones, and the other with y stones, what is the probability that George's corresponding piles are n-x and n-y respectively?
When this is true, this corresponds to a collision in the original problem.
In such a case, there are exactly 2*n stones altogether, and this is the only number of total stones in which a collision may occur.
Assuming both sides reach their destinations eventually, the total number of stones will go from 0 to 4*n eventually.
Therefore in all cases, the two players will cross that magical intersection of all states with 2*n total stones.
By symmetry, each must be equally likely, since we are given nothing in the problem to favor one such state over another.
Thus the answer is the number of states with 2*n stones where there is an collision divided by the total number of states with 2*n stones.
The collision states can be enumerated like:
(0,n,n,0)
(1,n-1,n-1,1)
(2,n-2,n-2,2)
...
...
(n-2,2,2,n-2)
(n-1,1,1,n-1)
(n,0,0,n)
Each is uniquely indexed by the first number in the tuple, which goes from 0 to n.
Hence there are n+1 collisoin states.
How many total 2*n states?
Assuming they travel at the same speed, each player must have the same number of stones i.e. n stones.
Well, George can divide his n stones however he pleases between the two piles: he has n independent binary decisions leading to 2^n possibilities.
Same with Lennie.
Lennie's binary decisions are independent with George's, so we have (2^n)*(2^n) = 2^(2n) possible 2*n stone states.
The answer is therefore (n+1)/(2^(2n))
Probabilities for n going from 0 to 20
0 : 1.01 : 0.52 : 0.18753 : 0.06254 : 0.019531255 : 0.0058593756 : 0.0017089843757 : 0.000488281258 : 0.0001373291015629 : 3.81469726562e-0510 : 1.04904174805e-0511 : 2.86102294922e-0612 : 7.7486038208e-0713 : 2.08616256714e-0714 : 5.58793544769e-0815 : 1.49011611938e-0816 : 3.95812094212e-0917 : 1.04773789644e-0918 : 2.76486389339e-1019 : 7.27595761418e-1120 : 1.90993887372e-11 -
we know it can't be the dual green card.
so it can either be blue,blue or blue,green.
i would tend to say 50/50.
your sample space isn't quite complete
-
Three bags are marked $10, $15, and $20. One bag contains two $5 dollar bills, one contains a $5 and a $10 bill, and one contains two $10 bills. You are told that no bag contains the amount of money that is marked on its exterior. You are allowed to select a bag and extract a bill. How many times must you do this before before you can guarantee that you know the contents of all three bags? What is your strategy?
-
A bag contains three cards, one blue on both sides, one green on both sides, and one with one blue side and one with one green side. You pull one card from the bag and place it on the table. The side showing is blue. What is the probability that the side not showing is also blue?
-
I would agree.
So would I.
i don't get it.. what if he goes for the one with 99 balls and gets a red ball?
Since all the red balls have to end up in some bucket, that the potential employer has the ability to choose, you cannot guarantee with probability 1 that he will draw a green ball.
The goal is to maximize that probability.
Using vistaptb's answer, you will get hired if the employer picks the bucket with the single green ball in it (he will pick that with probability 0.5). If he picks the other bucket, you will get hired with probability 49/99 = 0.49494949494949494949494949494949 ~ 0.5. He will pick this bucket with probability 0.5, so the net probability of you getting hired this way is 0.5*0.5 = 0.25.
Adding that to the 0.5 from the green ball, your chances of getting hired are approx 0.75.
When many people see this problem, the initial reaction is that it doesn't matter how you place them, it is always a 50% chance. This is not true, as shown above.
The intuition you should take from vistaptb's answer is that to minimize the effect of the red balls on probability, it is best to place as many green balls in the same bucket as the red balls, and that for other buckets, only a single green ball is needed to make the entire bucket a guaranteed win.
If we generalized the problem to n buckets, I haven't made a proof, but I think this strategy would also hold for any valid n.
The problem starts to seem different for n > 50 though, since at that point there would be some buckets with only red balls in them. Still given the situation, a strategy like the one above will still give the best of limited options I believe.
-
At a job interview, your potential employer presents you with the following test:
There are 2 buckets, and a bin with 50 green balls and 50 red balls.
He tells you he will leave the room, and that you must place the balls in the buckets.
When he comes back, he will randomly select a bucket (with equal probability), and randomly draw a ball from that bucket.
If he draws a green ball, you are hired.
Rules:
I. No bucket can be empty
II. Each of the 100 balls must be placed in one of the two buckets
What do you do?
-
What does F(0,0) evaluate to? you need it for F(1,1)
In case F(0,0)=1 then F(a,b) = b choose a, as in the binomial coefficient between b and a.
In case F(0,0)=0 then it's the binomial coefficient between b-1 and a.
Given F(0,0) there is only one solution, you can see this if you draw an xy axis and mark a on the x axis and b on the y axis, then mark 0's on the a axis and 1's on the b axis, then the value of every other point on the plane is the sum of values of the point to it's left and the point under that...
F(0,0) = 1
Sorry for leaving that out.
Nice work, you are correct!
-
Find a closed-form expression for F(a,b) where:
F(a,b) = F(a-1,b) + F(a-1,b-1),
F(a,0) = 1 for all a
F(0,b) = 0 for all b
a and b are positive integers
-
One more requirement for [A]: for finite sets, [A] = |A|
One more requirement:
If A is the real interval [0,1], and B = [0,0.5) U (0.5,1] U {2}
Then [A] =
B is the same as A, except that 0.5 is removed, and 2 is added.
B is no longer a subset of A, but from an intuitive perspective should have the same "quantity of points".
-
I don't think we can say the the same about the edge with respect to the cube:
The edge does not have other points than those contained in the cube.
Do you agree?
The subset operator would still show asymetry here.
The less-than operator would not show asymmetry between the cardinalities of the two sets.
Our intuition tells us, if A is a strict subset of B, then |A| < |B|.
Our conclusion from this discussion is that this transformation, from a statement of sets, to a statement of cardinalities, does not hold when sets are infinite.
Is there some other commonly accepted mathematical construct, e.g. denoted for set A by [A], that evaluates to a number, such that if A is a strict subset of B, then [A] < even for infinite sets?
One more requirement for [A]: for finite sets, [A] = |A|
-
So the cube has other points, but not more points.
I don't think we can say the the same about the edge with respect to the cube:
The edge does not have other points than those contained in the cube.
Do you agree?
The subset operator would still show asymetry here.
The less-than operator would not show asymmetry between the cardinalities of the two sets.
Our intuition tells us, if A is a strict subset of B, then |A| < |B|.
Our conclusion from this discussion is that this transformation, from a statement of sets, to a statement of cardinalities, does not hold when sets are infinite.
Is there some other commonly accepted mathematical construct, e.g. denoted for set A by [A], that evaluates to a number, such that if A is a strict subset of B, then [A] < even for infinite sets?
-
If extra, or better, other, were used in OP, the answer would be Yes.
But with more, as in OP, the answer is No.
But it's best to say the points in the cube and its edge have the same cardinality. That gets us off the hook a little, because cardinality is a well behaved algebraic number only for finite sets. For infinite sets, Aleph0, Aleph1, Aleph2, are symbols that are not like algebraic symbols. Specifically, they are invariant to addition, multiplication, squaring, cubing ...
Aleph1 == Aleph1 + 1 == Aleph1 x Aleph1 == ... And so forth.
That's why asking questions about the Alephs that include words like "more than" lead to counterintuitive results.
But 2Aleph1 == Aleph2.
That is, the set of all subsets [power set] of an infinite set jumps up to the next higher cardinality. The proof that the elements of any set can not be paired 1-1 with the elements of its power set is both simple and elegant.
Cantor [can't or] originally thought Aleph1 x Aleph1 would lead to Aleph2. That is, the points in a plane would have next higher cardinality than the points in a line. And a cube would have the next higher cardinality than the plane. And so on.
But when he tried to show this, he instead proved all three cardinalities were the same. Much to his surprise, and now to ours.
So the point of this puzzle was to pause and wonder at the result that adding and multiplying, squaring or cubing do not affect the cardinality of infinite sets.
And that result can be shown, as Bushindo did, by finding a bijection between the cube and an edge.
using bushindo's method, we can represent n real numbers (a vector) using a single real number for any finite n.
each element of such a vector is also a real number, and can therefore represent another vector of real numbers.
following along these lines, any real tensor can be uniquely mapped to a single real number.
a single real number, therefore has the same level of complexity as a 100 by 100 by 100 tensor of arbitrary real numbers (i.e. they can be used interchangeably to communicate the same thing).
practically any set of data one could ever want to use or interact with, regardless of how large, could be encoded as a single numerical position on a number line (with higher precision required for more info).
forget about achilles passing the tortoise... what about when he passes the point on the racetrack whose real position contains all of the data in his genetic makeup under an encoding scheme like the one bushindo showed?
that is far more interesting!
-
choice
It is an axiom - the axiom of choice (well... maybe it is)...!
Here is my attempt at connecting the two ideas.
http://en.wikipedia....Axiom_of_choice
Here is a variant:
"Given any set X of pairwise disjoint non-empty sets, there exists at least one set C that contains exactly one element in common with each of the sets in X."
Treating a triplet of digits at positions (k,k+1,k+2) for k = floor(n/3)+1 (where the 10^0 decimal is at position 0) in bushindo's e as the C above and X as the set containing the nth digits of x,y, and z, the axiom of choice guarantees bushindo's construction exists.
I'm not sure how to prove that if the axiom of choice is not taken, that bushindo's construction cannot certainly be constructed... so maybe i am wrong here.
i am assuming ordered sets (tuples), so that is slightly different than the statement of the axioms of choice i have.
but if i am right, then the title of this thread is actually relevant

http://en.wikipedia....ki/Ordered_pair
"In 1921 Kazimierz Kuratowski offered the now-accepted definition[4] of the ordered pair (a, b):
 "
"let x be the set of ordered pairs (v,n) where n is an integer indicating the position of a digit, and v is the digit itself.
an ordered triplet (a,b,c) can be defined as (a,(b,c)) = {{a},{a,(b,c)}} = {{a},{a,{{b},{b,c}}}}
so given n, to construct the triplet C_n = (x_n,y_n,z_n) = {{x_n},{x_n,{{y_n},{y_n,z_n}}}}, we must be able to select:
{{x_n},{x_n,n}} from x
{{y_n},{y_n,n}} from y
{{z_n},{z_n,n}} from z
i.e. elements from x,y,z where the second value in the ordered pair equals n.
by the way we have defined things, such an element must always exist for x,y, and z and any n, so i don't see why we wouldn't be able to select it.
the only time i have seen (in my limited experience) where the axiom of choice actually plays a useful role is when there is some sort of indistinguishability between multiple things, and the axiom of choice kicks in to say, even though these things are indistinguishable, you can still pick one.
by the way we defined this, i don't see any indistinguishability.
we could even guarantee that x,y, and z distinguishable, by making them ordered pairs themselves and putting some identifier (e.g. 1 for x, 2 for y, 3 for z) as the first element of the ordered pair, and then previously described countably infinite set of natural numbers as the second element of the pair.
so maybe the axiom of choice doesn't apply here....
on the other hand... the AC is equivalent to the well-ordering theorem in first order logic, and perhaps we somehow implicitly assumed that in our construction of these real numbers.
i think i've probably reached the limit in what i know about this topic (as well as the limit of the time i have to spend on this tonight), so hopefully someone else can step in and show the light.
-
sorry, thought a little more, wanted to write a little more
is being able to form a 1-1 mapping really equivalent to having the same number of things?
obviously yes for the finite case
in the infinite case, it seems to me that this definition of cardinality is more like: starting from the cube set or the edge set, there are always enough available point resources in the other set to support a mapping no matter how many points you ask for a partner for (i.e. there exists an injective mapping).
this doesn't to me seem to mean that when you have paired all the points in your starting set, that there are no longer any point resources in the other set left (and are therefore unpartnered) i.e. does not imply that the mapping is surjective.
to prove surjectivity, for example in bushindo's case, you invert the algorithm and show that it is injective when starting from the other set as well.
the crux of the counter-intuitiveness is that one real number, can contain the information of three real numbers, as bushindo showed.
what if there is an infinite amount of information? (by information i mean the ordered set of decimal digits making up a number) ----> what if x=y=z=pi or some other transcendental number?
i guess e would be another transcendental number, but everything would still work.
but this almost seems like it's cheating. logically what we are doing is mapping one number to three numbers using a clever encoding scheme.
any real number can be thought of as an infinite ordered set of natural numbers (the digits of the number).
by saying we can construct the number e, from numbers x,y, and z, we are implicitly assuming that e has the capacity to store x, y, and z.
this assumption is logically equivalent to the conclusion that a single edge has the capacity to provide partner points to every point in a cube.
doesn't that make assuming that e can be constructed from x,y, and z, to prove that edge and cube cardinalities are the same, a circular fallacy?
if we are not allowed to assume that e has the capacity to completely store x, y, and z, but rather the capacity to store only one of them, then I think we would conclude the cardinality of the cube is greater than the edge.
so how do we prove that e can be constructed for any real x,y,z?
perhaps the argument is, I can try to construct it and I know what I would do at every step, so therefore it is constructable?
but if x,y, or z is transcendental, then such a construction would never end....
well at least it couldn't be described in terms of a simple repetitive instruction loop (e.g. the rest of the digits are all zero, or the rest of the digits are 142857 repeating). i suppose it's always an infinite construction even in the simplest of cases.
perhaps the concept that a single real number can store the information of an arbitrary number of other real numbers is an axiom rather than something proven from simpler axioms. if that is the case, then the original question is essentially asking whether we choose to adopt this axiom or not.
anyone care to offer some help?



find last two digit
in New Logic/Math Puzzles
Posted
20
because python
def nnmod100(n):
nm = n % 100;
p = 1;
for i in xrange(n):
p = (p*nm) % 100;
return p;
s = sum(nnmod100(n) for n in range(1,100));
print s % 100;