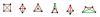plasmid

It doesn't matter what random number generation method you use, the results will be the same. And there's no need to code the program if you can tell by looking at it what the results would be.

The experiment is fairly simple. Randomly generate howevermany "smaller" envelopes you want {s1, s2, s3 ... sn} and for each of them generate a matching "greater" envelope {g1, g2, g3 ... gn} where the value in gx = 2sx. Let the value of all sx and gx be small relative to the bank account. The participant is given a random envelope and given the choice of whether or not to switch -- if he was originally given an envelope sx then he will switch to envelope gx, and if he was originally given an envelope gy then he will switch to envelope sy. Now compare what happens if the participant takes a strategy of switching vs a strategy of staying with the initial envelope. The probability distribution is random, and results should generalize to any probability distribution that you face. One could argue that it doesn't fit the OP because the player isn't presented a value of $1000. I would counter that the precise value that the player finds when he opens the envelope is arbitrary (you could multiply all of the s and g terms by any value you like) and would not affect the conclusions of the experiment.

I believe there is a good reason why a probability distribution was not stated in the problem. I can think of an "experiment" that I believe would be considered satisfactory by most people, that doesn't depend on the probability distribution of how much money is in the smaller or larger envelope. The answer would be appropriate if our only information were that $1000 is small compared to the available bank account (ruling out the trivial possibility that the bank account is less than $3000 which would make it impossible for the other envelope to hold $2000 and obvious that you should not switch).

Morningstar: what would happen if you changed your program so the amount of money in the first envelope was random? And would that prove that it's always better to switch from whichever envelope you're looking at? Bushindo: It's certainly better to not switch if you know that there is a ceiling for how much money could be in an envelope and you see an envelope containing more than half of that. But the problem doesn't make any mention of a ceiling. And it may very well be that you don't know how much money is in the bank account, or even if you did then you know that the amount of money in the envelopes is small compared to the size of the bank account but not precisely how small. That might lead one down the road of looking for a probability distribution with an interesting property. But a complete answer to the question should take into account that the probability distribution could be anything.

Can you gain as much by switching back? Using the same reasoning? There is a paradox: A gain for switching can be anticipated. Yet, there is a preferred envelope, and if we initially chose it we should not switch. Not sure what you mean by "switching back". The 50/50 comes from randomly picking one of 2 envelopes from which we know one has double the money of the other. I don't see a paradox. The paradox comes from the fact that $1000 is arbitrary.Suppose I were to point to an envelope before any were opened, and I said "That envelope contains some amount of money; call it $X. The other envelope therefore must contain $2X or $X/2." You could now argue that the expected earnings from picking the other envelope are $5X/4, so you should choose the other envelope. But in reality, have I actually given you any more information than you already had when you only knew that one envelope contains twice as much money as the other?

Let's see who can tell us what's wrong with this line of reasoning. First, consider the case where the amount of money in the envelope could be any real number, not restricted to integers or whole cents. Next, consider the case where the amount of money in the envelope must be some integer value of dollars and/or cents. Let us also assume for the sake of the problem that there is an equal probability that the smaller envelope contains any possible amount of money, odd or even. I believe this proves all possibilities: one where you're more likely to have the smaller amount of money, one where you're more likely to have the larger amount of money, and one where they are equally likely.

Doesn't the "one and only one of us will ever tell you the truth" interpretation mean that it's possible for all three of the people in the first group to be liars?

I remember this one. Admittedly something that cannot really be found using a search... unless you know that that version had "sword" and "kill", and you're willing to look through a few pages of search results.

I see what tripped me up. I interpreted 382's statement as "exactly one of us tells the truth", and not "no more than one of us tells the truth". That would allow 382 to be a liar if all three of the initial group were liars.

I don't know about everyone else, but I'm stuck. If the "I" in this problem has information that we (the problem solvers) are not privy to by virtue of the OP, then I could come up with a solution. If the "I" in this puzzle definitely does NOT have any more information than what's presented, then I am Stuck with a capital S.

How about two more, which are rather mother-centric:

I'm coming up with an answer that makes me think my analysis is just a little off.

Not sure if this was the same process that jhawk used, but it's what I would have done if it weren't already answered. And it doesn't seem to involve freezing.

The shortest and most intuitive (although least formal) proof of the answer that I can come up with.

I'm not taking the last spot. I'm leaving it open for newbies and will be available to jump in as a backup if anyone's inactive.

I would volunteer to take the last spot to get the game started, but I don't know if Minato is still following. You could try PM-ing, and if Minato is still around and would be able to play I can take spot 6. Otherwise, I foresee needing a backup.

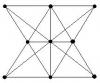
I've been stuck on this one. Maybe it would help to know whether or not the following figure is a subset of the final answer, since I keep coming back to it and it seems to at least be a local minimum (or whatever the appropriate term would be)

Ah, I see... a pentagon minus one point. Which I guess would be the only answer if there were five points instead of four.

I can prove it, although it's a bit brutish.

Without any sort of formal proof, I think that these are all possible shapes. Although I haven't yet fully convinced myself that the last shape I drew actually exists. It seems like it should though.

Principals: Auramyna & Brainiac100 1. Flamebirde 2. 3. 4. 5. TheCube 6. 7. Minato 8. marksmanjay 9. 10. 11. Backups 1. plasmid If signups get close to full and then stall, you can make me a player to get the game started. But I'd rather let it actually be a newbie mafia.