bushindo

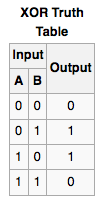
In binary modular arithmetic, y XOR An y is indeed equivalent to (y - An y), as the following table will show Notice that for a and b in the discrete set (0, 1), (a XOR b) is indeed equal to (a + b) mod 2.

Here's an upper bound on the largest row length for which the first player can win

I'm afraid I don't follow this post. With the last sentence, did you mean to say, it is now y - A^n y, or it is not y - A^n y ?

Adding more hints for completing the proof. See post above for background.

There's another

It should be equal to

Adding additional hints for proving that the optimal strategy described by araver and superprimastic will guarantee a win

Using the proof technique that I posted in post #8, I was able to verify that this strategy would also guarantee that we would win in the end. Good work!

Araver and superprimastic got the correct strategy ( nice analysis and intuition, araver). I'm interested in seeing more of superprimastic's input after the hurricane (be safe). As for me, I was able to prove that the strategy is guaranteed to win using

That is correct. The Butler may turn the table in any direction and for as many spaces as he wants.

Let's say that you are setting the dining table for a party of 64 guests. The 64 guests will be seated at a giant circular table. Each seat has a lamp, and currently some of the 64 lamps are on and some are off. The butler offers to play a game with you. Let's say that the chairs are labelled with the guests names, which for convenience we label starting from the top and going clockwise as G1, G2, ..., G64, and the chairs are stationary. The giant circular dining table along with the lamps, however, can rotate. Each lamp has a switch, and flipping the switch when the lamp is on turns it off, and vice versa. The game is as follows 1) The game consist of turns. At each turn, you tell the butler a list of chairs at which you want to switch the lamps' state. 2) The butler will then has the option of arbitrarily rotating the entire table before he apply the switches at the list of chairs in point 1). Please note that the butler must rotate the table in such a way that each chair is directly across from a lamp (rotating so that a lamp ends up midway between two chairs isn't allowed). 3) You may take as many turns as you'd like. If you succeed in turning all the lights on, you win. Example: Let's say that currently all lamps are off except for the ones at G1, G3, and G5. You tell the butler to switch the lamps at G1, G3, and G5. The butler then rotates the table counter-clockwise 2 spaces. Now, the lamps at seats G63, G1, and G3 are on. The butler then proceed to switch the lamps at G1, G3, and G5. The end result is that now the lamps at G63 and G5 are on. Show that there's a strategy that is guaranteed to turn all the lamps on.

Yup, perfect solution. It's nice to see you around this New Puzzles forum once more. Reminds me of the grand old time when we solved 'Team of 15' together. Good old times =)

// I'm going to come out and admit that the phrase '4 or less correct' is a red herring =). I have a winning rate of 2/3, and I believe avaver and molly are on a cusp of getting that solution.

*Sign*, the brainden never ceases to amaze me with the out-of-the-box solution. Congratulations, you win the out-of-the-box solution. There's still the intended in-the-box solution where each person can only write down Red, Black, or White. No one has that solved yet.

Since you are interested in the 'fastest' algorithm, an computational complexity analysis is in order

How about this strategy

It is indeed as you say. If 0, 1, 2, 3, or 4 people got their color correctly, then everybody wins. Any more than that and they all go back to the death row.

Actually, you are right about the winning chance. I made a mistake in phrasing this puzzle. The condition should have been 'If 4 or less people got their hat color correct, then everybody wins.' In the incorrectly quoted version, the ideal solution is pretty much as you say. I fixed the wording the the original post.

<p> </p> <p> </p> <p> </p> <p>Actually, you are right about the winning chance. I made a mistake in phrasing this puzzle. The condition should have been 'If 4 or less people got their hat color correct, then everybody wins.' In the incorrectly quoted version, the ideal solution is pretty much as you say. I fixed the wording the the original post.</p>

Here is an interesting twist to this puzzle

Let's say that you and 27 other prisoners are on a death row. The warden gives you and your fellow prisoners a chance to win your freedom through a game. The game is as follows, 1) When the game starts, the warden will blindfold all 28 prisoners and arrange them in a circle. 2) The warden will put on each prisoner's head either a RED, BLACK, or WHITE hat. The warden will choose the color for each prisoner uniformly by tossing a fair die. 3) The warden will then remove the blindfolds. Every prisoner will be able to see the hats on the other 27. Each person will not know the color of his own hat. 4) The warden then gives everybody 1 minute so that each person can think about what his hat color is. At the end of that 1 minute, the warden will provide each prisoner with some paper, and all 28 prisoners must write their hat color at the same time. If 4 or less people got their hat colors correct, then everybody win their freedom. Otherwise, they all go back on the death row. 5) Each person is absolutely not allowed to communicate with his fellow prisoners during the game by speaking, facial expressions, body language, etc. The warden reserves the right to cancel the game and put everybody back on the death row if he see these types of behavior. You and your 27 friends have 1 night to discuss a strategy. Find a strategy that makes your chances of freedom as high as possible. EDIT: fixed a wording mistake that was pointed out by smoth333

Congratulations to CaptainEd and witzar for the nice solve. I'm glad you enjoyed the puzzle. I'm working on another one and will post it soon.

I think this would violate provision 5) in the OP, which states that each person is not allowed to communicate to his fellow prisoners during the game by varying his tone of voice, volume, facial expressions, body language, etc. Also, please consider using spoiler for your answers since other people may want to work on the solution on their own. This is a huge improvement over the previous bar set by Molly. It is still sub-optimal, although you're approaching the ceiling

Your strategy is not optimal yet. It is a good beginning step, though You found a loophole that I didn't think about when I tried to box the out-of-the-box solutions. Having a choice of which arm to raise is not intended in the OP, however, I don't see how it can help improve the winning rate beyond strategies like Molly Mae's. Can you flesh out your strategy so that we can compute a winning rate?

Let's say that the clocks have non-reflective surfaces. Nice out of the box thinking, though. Hope this Helps and I think this would work? (Well I hope it would anyway) This is also interesting out of the box thinking. However, let's assume that each prisoner is required to shout his hat color at the same instant that he raises his hand.