bonanova

Inspired by BMAD's puzzle, consider choosing four random numbers on [0,1]. If you sort them lowest to highest, what is the expected value of the third number?

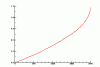
I think we both have the entire playing field covered. My view of the field includes "canonical" numbers generated from p and q. It also includes "anomalous" numbers that arise from non-canonical roots (11, 23, 181,...) whose squares (121, 529, 32761, ...) are canonical. The convergent roots each spawn an infinite family of other convergent numbers. I've been working from a sketch of the field, below, that shows "anomalous" numbers and the recursion formula in red. The sketch shows how and where they branch into the canonical field. The anomalous numbers seem to attach to alternating branches and with alternating parity of powers of 2. That may be a coincidence, but I think it would be interesting to find the next odd square that has canonical form. Can you think of other places to search?

It's lower than that.

I match your list of divergent numbers. I decided to increase the range to 1000. Convergent numbers become the minority pretty quickly, so I tabulated them, instead of the divergent numbers. There are 286. Convergent numbers from 2 TO 1000 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 28 29 30 31 32 33 34 35 36 37 38 40 41 42 44 45 46 47 48 49 50 52 56 57 58 60 61 62 63 64 65 66 67 68 69 70 72 73 74 76 80 81 82 84 88 89 90 92 93 94 96 97 98 100 104 112 113 114 116 120 121 122 124 125 126 127 128 129 130 131 132 133 134 136 137 138 140 144 145 146 148 152 160 161 162 164 168 176 177 178 180 184 185 186 188 192 193 194 196 200 208 224 225 226 228 232 240 241 242 244 248 249 250 252 253 254 255 256 257 258 259 260 261 262 264 265 266 268 272 273 274 276 280 288 289 290 292 296 304 320 321 322 324 328 336 352 353 354 356 360 363 368 369 370 372 376 384 385 386 388 392 400 416 448 449 450 452 456 464 480 481 482 484 488 496 497 498 500 504 505 506 508 509 510 511 512 513 514 515 516 517 518 520 521 522 524 528 529 530 532 536 544 545 546 548 552 560 576 577 578 580 584 592 608 640 641 642 644 648 656 672 704 705 706 708 712 720 725 726 736 737 738 740 744 752 768 769 770 772 776 784 800 832 896 897 898 900 904 912 928 960 961 962 964 968 976 992 993 994 996 1000. In this list there are three numbers that I did not find using my current method. The numbers are 363, 725 and 726 (which is 2x363.) 363 and 725 converge, following the squares of : 181 4095 2047 1023 511 255 127 63 31 15 7 3 1. 1812 = 32761 = 1 + 32768 - 8 which is canonical form. That uncovers a third set of anomalous convergent numbers. They are: 11x11 = 121 = 1 + 128 - 8. Spawns 23 45 89 177 353 705 1049 2817 5633 ... 23x23 = 529 = 1 + 512 - 16. Spawns 47 93 185 369 737 1473 2945 5889 ... 181x181 = 32761 = 1 + 32768 - 8. Spawns 363 725 1449 2897 5793 ... and their powers-of-2 multiples, like 726 above. I'm more firmly convinced this is a complete set of convergent numbers. Convergent numbers get increasingly sparse in the high-number range. The anomalous ones are an increasingly sparse subset: 11 - 23 - 181 - ? The only other type anomaly I can imagine is one where O must be applied twice (or more) to get to canonical form. It would be interesting to write a program to find all the odd squares that have canonical form, and the numbers they spawn. I don't think there are many. OK that was a dumb statement. They are probably infinite. But very sparse. I agree that none of this is a proof.

Right. It's (a+b)(c+d) - ac - bd.

plasmid, I went over my stuff tonight and found the number 23 also. That number, and 47 and a few others, converge for a simple reason explained in the spoiler, and I think that makes the list complete. However, I would love to learn of any other mavericks or, even more interestingly, any other generating equation.

I knew I was missing something obvious. I'll take slight credit for purposefully obfuscating that precise point (no two cards in a deck have ...) Heh.

Trying to help with the difficulties of language ... Should we find a triangle, that meets the conditions, that has a side that is smaller then the smallest side of any other triangle that meets the conditions?

Reminds me of an old song, "I'm my own Grandpa." Work it both ways, regular and special. How few can it get?

At a family party, a grandfather, a grandmother, two fathers, two mothers, four children, three grandchildren, one brother, two sisters, two sons, two daughters, one father-in-law, one mother-in-law, and one daughter-in-law, sit at a table. What is the fewest number of chairs required to seat all of them? Each had his/her own chair.

Moe and Joe had some time on their hands, so they played a simple game called "Dueling Cards." In this game, each player has a deck of cards, shuffled and without jokers. A hand consists of a single card taken from the top of each player's deck. Suits and face values are both ranked. No two cards in a deck have the same rank. A player wins the hand by holding a card that outranks the card of his opponent. The bank pays 1 chip to the winner of a hand. It's a simple game. No poker hands. No betting. Just high card wins. After 52 hands the decks are re-shuffled, and play continues as long as desired. Moe and Joe played through their decks 10 times, then stopped to see who won. As they counted their chips Moe (a statistician) said, I wonder what the most likely winning score is. Joe (a simpler person) replied, I wonder what the most likely combined score is. I'm sure Bushindo can answer Moe's question. I can't. So instead this puzzle asks Joe's question.

There is a straightforward procedure for this.

I think LVan Toren has it. NIce!

The issue here is fairness for all the 4 guests/cutters ..and it is still fair for all if the remaining piece on the tray has the same flavor,volume ,weight yet not the same shape like the pieces on the plates. OK, so the question is, and we're all anxious to know ... has the puzzle been solved? And if not, what is missing from dgreening's solution?

You must be a mathematician. "This reduces to the previous case."

If exact results are required I agree. I can't imagine how without a scale or other way to verify. If OP requires similar and fair, it has the same flavor as the I cut - you choose n=2 case. With regard to specifics, Flavor - seems automatic. Sounds like it might even be tongue in cheek (pun intended.) Size and weight go together - each person does a visual inspection. Shape is satisfied by cutting wedges from the center.