Sliding spheres

[bonanova]

A sphere of radius R=1 sits on the x-y plane at its origin. A second sphere of radius r<<1 is balanced on top of the first. That is, their centers are at [0, 0, 1] and [0, 0, 2+r] respectively. The surfaces are frictionless.

A butterfly in the Amazon Forest imparts to the top sphere the slightest of horizontal velocities, causing it to slide downward along the surface of the bottom sphere. At one point the spheres break contact. At a later point the smaller sphere lands on the x-y plane.
 

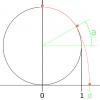
• At what north latitude on the bottom sphere do they break contact?
  That is, how many degrees a above the bottom sphere's equator.
   
• At what distance d from the origin does the smaller sphere land on the plane?

Edited September 25, 2014 by bonanova
Add figure

[karthickgururaj]

 

 

Assuming R = 1 meter

 

At point of separation, the following conditions hold:

a. Velocity of the second sphere is 'v' (will be tangential to the first sphere's surface), where 'v' can be calculated from loss of potential energy:

   v² = 2.g.(r - r.sin(a)), where r = 1 is the radius of the first sphere

b. Further, the centrifugal force must cancel out the component due to gravity, yielding:

   g.sin(a) = v²/r

 

Hence, sin(a) = 2.(1-sin(a)) => a ~ 0.34 radians = 19.47^o

 

Also, we can get the value of 'v' as: v²/1 = 9.8*1/3 => v = 1.81 m/s

 

 

Not quite ... a mistake solving for sin(a).

 

 

Time taken for the ball to fall down a height = h = r + r.sin(a), starting with an initial velocity of v.cos(a) will be, 't' such that,

 

   r + r.sin(a) = v.cos(a).t + (1/2).g.t²

 

Putting the values for v, r, g and a and solving the quadratic for t and eliminating the negative value, we get t = 0.376 sec

 

In that time, the ball will travel horizontally for t.r.sin(a) = 0.125.

 

So d = r.cos(a) + 0.125 = 1.0678

 

 

Right approach.

 

Eeek. Sorry.. This is why we still need pen and paper.

 

 

sin(a) = 2/3 => a ~ 0.73 radians or 41.81^o

 

v² = 9.8*2/3 => v = 2.56 m/s

 

The quadratic in t then becomes:

 

1 + (2/3) = 2.56*0.745*t + (1/2)*9.8*t² => t = 0.42 sec.

 

Horizontal travel = t.r.sin(a) = 0.42*1*(2/3) = 0.28 m

 

d = r.cos(a) + 0.28 = 1*0.745 + 0.28 = 1.025 m

 

[karthickgururaj]

Assuming R = 1 meter

 

At point of separation, the following conditions hold:

a. Velocity of the second sphere is 'v' (will be tangential to the first sphere's surface), where 'v' can be calculated from loss of potential energy:

   v² = 2.g.(r - r.sin(a)), where r = 1 is the radius of the first sphere

b. Further, the centrifugal force must cancel out the component due to gravity, yielding:

   g.sin(a) = v²/r

 

Hence, sin(a) = 2.(1-sin(a)) => a ~ 0.34 radians = 19.47^o

 

Also, we can get the value of 'v' as: v²/1 = 9.8*1/3 => v = 1.81 m/s

 

 

 

Time taken for the ball to fall down a height = h = r + r.sin(a), starting with an initial velocity of v.cos(a) will be, 't' such that,

 

   r + r.sin(a) = v.cos(a).t + (1/2).g.t²

 

Putting the values for v, r, g and a and solving the quadratic for t and eliminating the negative value, we get t = 0.376 sec

 

In that time, the ball will travel horizontally for t.r.sin(a) = 0.125.

 

So d = r.cos(a) + 0.125 = 1.0678

 

 

 

[bonanova]

 

Assuming R = 1 meter

 

At point of separation, the following conditions hold:

a. Velocity of the second sphere is 'v' (will be tangential to the first sphere's surface), where 'v' can be calculated from loss of potential energy:

   v² = 2.g.(r - r.sin(a)), where r = 1 is the radius of the first sphere

b. Further, the centrifugal force must cancel out the component due to gravity, yielding:

   g.sin(a) = v²/r

 

Hence, sin(a) = 2.(1-sin(a)) => a ~ 0.34 radians = 19.47^o

 

Also, we can get the value of 'v' as: v²/1 = 9.8*1/3 => v = 1.81 m/s

 

 

Not quite ... a mistake solving for sin(a).

 

 

Time taken for the ball to fall down a height = h = r + r.sin(a), starting with an initial velocity of v.cos(a) will be, 't' such that,

 

   r + r.sin(a) = v.cos(a).t + (1/2).g.t²

 

Putting the values for v, r, g and a and solving the quadratic for t and eliminating the negative value, we get t = 0.376 sec

 

In that time, the ball will travel horizontally for t.r.sin(a) = 0.125.

 

So d = r.cos(a) + 0.125 = 1.0678

 

 

Right approach.

[bonanova]

Of the two questions I asked, the first is the more elegant. The answer (contact angle) is the same for any size sphere or any planet. So long as the planet's mass is large compared to that of the sphere. The second question seemed reasonable to ask, and it surprised me a little that its answer (landing point) does depend on size and on gravitational pull. On Earth, the result shows that the apple does not fall far from the tree. I also heard someone remark that the angle (in degrees) is strikingly close to the answer to life and everything. See Hitch-hiker's guide to the galaxy.